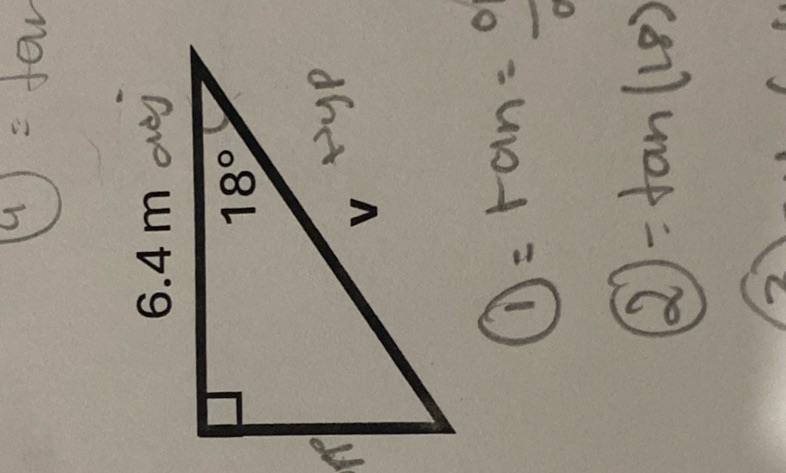
Question: The image shows a right-angled triangle with the following annotations: - One side is labeled as…

The image shows a right-angled triangle with the following annotations:

• One side is labeled as \( 6.4 \, \text{m} \).
• The angle opposite the side labeled \( 6.4 \, \text{m} \) is \( 18^\circ \).
• The triangle is right-angled at the bottom left corner.

Additionally, there are some handwritten notes around the triangle, including:

• \( \tan = \frac{\text{opposite}}{\text{adjacent}} \)
• \( \tan = \frac{6.4}{\text{adjacent}} \)
• \( \tan(18^\circ) = \frac{6.4}{\text{adjacent}} \)

These notes suggest that the problem involves using trigonometry to find the length of the adjacent side of the triangle.

Solution

To find the length of \( v \) in the right triangle, we can use the sine function of the given angle, since we have the opposite side and are looking for the hypotenuse. The formula for sine is: \[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \] Substitute the known values into the formula: \[ \sin(18^\circ) = \frac{6.4}{v} \] Solve for \( v \): Multiply both sides by \( v \): \[ v \cdot \sin(18^\circ) = 6.4 \] Divide both sides by \( \sin(18^\circ) \): \[ v = \frac{6.4}{\sin(18^\circ)} \] Now calculate: \[ v \approx \frac{6.4}{0.3090} \approx 20.71 \] Therefore, the length of \( v \) is approximately 20.71 meters.