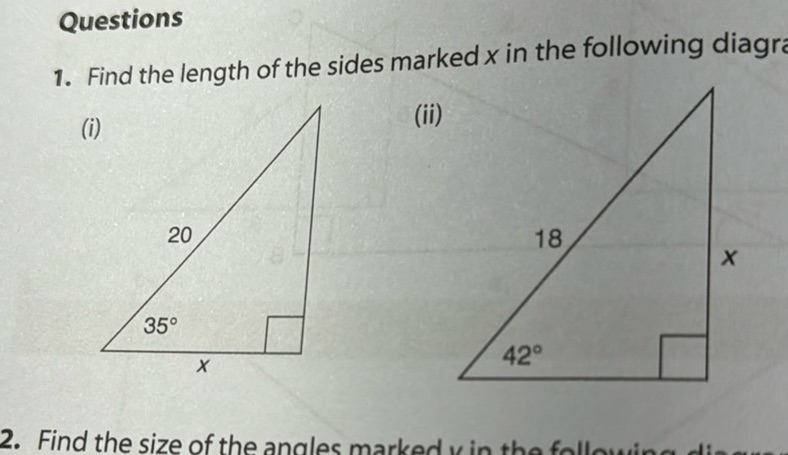
Question: Questions 1. Find the length of the sides marked \( x \) in the following diagrams: (i) \[…

Questions

1. Find the length of the sides marked \( x \) in the following diagrams:

(i) \[ \begin{array}{c} \text{20} \\ \text{35}^\circ \\ x \end{array} \]

(ii) \[ \begin{array}{c} \text{18} \\ \text{42}^\circ \\ x \end{array} \]

2. Find the size of the angles marked \( y \) in the following diagrams:

Solution

Problem 1(i): Find the length of the side marked \( x \) in a right triangle with a hypotenuse of 20 and an angle of \( 35^\circ \). Step 1: Use the sine function \[ \sin(35^\circ) = \frac{x}{20} \] Step 2: Solve for \( x \) \[ x = 20 \times \sin(35^\circ) \] Step 3: Calculate \( x \) \[ x \approx 20 \times 0.5736 = 11.47 \] So, \( x \approx 11.47 \) units. --- Problem 1(ii): Find the length of the side marked \( x \) in a right triangle with a side length of 18 and an angle of \( 42^\circ \). The side adjacent to the \( 42^\circ \) angle is marked as \( x \). Step 1: Use the tangent function \[ \tan(42^\circ) = \frac{18}{x} \] Step 2: Solve for \( x \) \[ x = \frac{18}{\tan(42^\circ)} \] Step 3: Calculate \( x \) \[ x \approx \frac{18}{0.9004} \approx 19.99 \] So, \( x \approx 20 \) units.