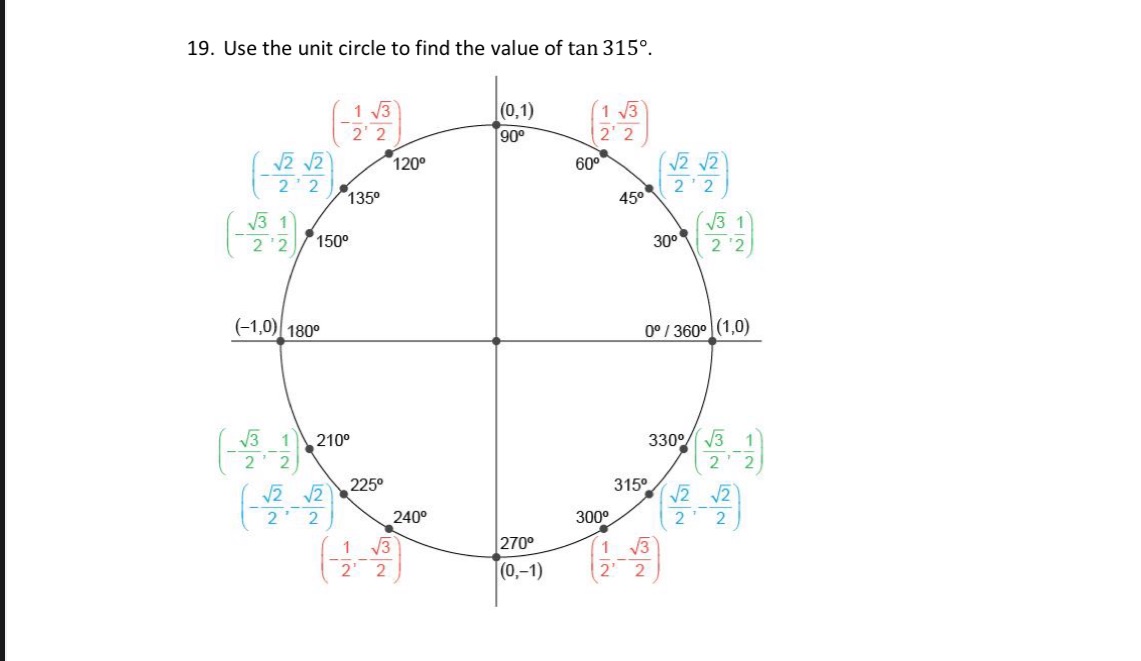
Question: 19. Use the unit circle to find the value of $\tan 315^\circ$. The unit circle is shown with…

19. Use the unit circle to find the value of $\tan 315^\circ$.

The unit circle is shown with various angles and their corresponding coordinates:

• $0^\circ / 360^\circ$: $(1, 0)$
• $30^\circ$: $\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$
• $45^\circ$: $\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$
• $60^\circ$: $\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$
• $90^\circ$: $(0, 1)$
• $120^\circ$: $\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$
• $135^\circ$: $\left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$
• $150^\circ$: $\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$
• $180^\circ$: $(-1, 0)$
• $210^\circ$: $\left(-\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$
• $225^\circ$: $\left(-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right)$
• $240^\circ$: $\left(-\frac{1}{2}, -\frac{\sqrt{3}}{2}\right)$
• $270^\circ$: $(0, -1)$
• $300^\circ$: $\left(\frac{1}{2}, -\frac{\sqrt{3}}{2}\right)$
• $315^\circ$: $\left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right)$
• $330^\circ$: $\left(\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$

Solution

To find the value of \(\tan 315^\circ\) using the unit circle, follow these steps: Locate the point on the unit circle corresponding to \(315^\circ\). The coordinates for \(315^\circ\) are \(\left( \frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \right)\). The tangent of an angle \(\theta\) is given by the ratio of the \(y\)-coordinate to the \(x\)-coordinate: \[ \tan \theta = \frac{y}{x} \] Substitute the coordinates into the tangent formula: \[ \tan 315^\circ = \frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} \] Simplify the expression: \[ \tan 315^\circ = -1 \] Therefore, the value of \(\tan 315^\circ\) is \(-1\).