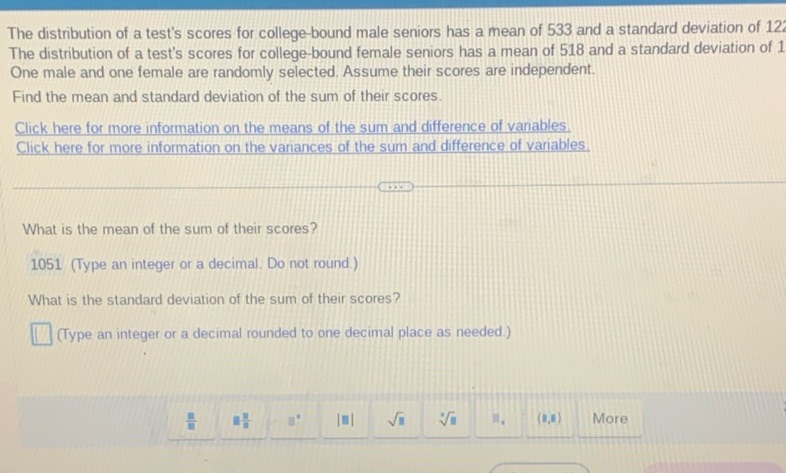
Question: The distribution of a test’s scores for college-bound male seniors has a mean of 533 and a standard…

The distribution of a test’s scores for college-bound male seniors has a mean of 533 and a standard deviation of 122. The distribution of a test’s scores for college-bound female seniors has a mean of 518 and a standard deviation of 110. One male and one female are randomly selected. Assume their scores are independent.

Find the mean and standard deviation of the sum of their scores.

What is the mean of the sum of their scores?

1051 (Type an integer or a decimal. Do not round.)

What is the standard deviation of the sum of their scores?

(Type an integer or a decimal rounded to one decimal place as needed.)

Solution

Step 1: Identify the means and standard deviations of the individual scores. Mean of male scores, \(\mu_1 = 533\) Mean of female scores, \(\mu_2 = 518\) Standard deviation of male scores, \(\sigma_1 = 122\) Standard deviation of female scores, \(\sigma_2 = 117\) Step 2: Calculate the mean of the sum. \[ \mu_{\text{sum}} = \mu_1 + \mu_2 = 533 + 518 = 1051 \] Step 3: Calculate the variance of the sum. \[ \sigma_{\text{sum}}^2 = \sigma_1^2 + \sigma_2^2 = 122^2 + 117^2 = 14884 + 13689 = 28573 \] Step 4: Calculate the standard deviation of the sum. \[ \sigma_{\text{sum}} = \sqrt{28573} \approx 169 \] The standard deviation of the sum of their scores is approximately 169.