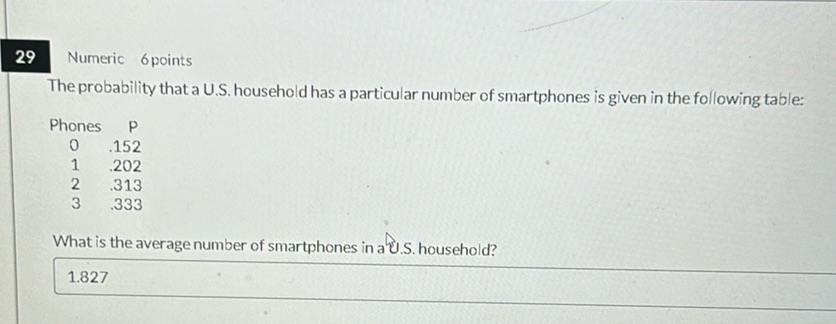
Question: Numeric 6 points The probability that a U.S. household has a particular number of smartphones is…

Numeric 6 points

The probability that a U.S. household has a particular number of smartphones is given in the following table:

Phones P 0 .152 1 .202 2 .313 3 .333

What is the average number of smartphones in a U.S. household?

1.827

Solution

To find the average number of smartphones in a U.S. household, we need to calculate the expected value of the distribution. The expected value \(E(X)\) is given by the sum of each value multiplied by its probability. Let \(X\) be the random variable representing the number of smartphones. We need to calculate: \[ E(X) = 0 \times 0.152 + 1 \times 0.202 + 2 \times 0.313 + 3 \times 0.333 \] Calculate each term: \[ 0 \times 0.152 = 0 \] \[ 1 \times 0.202 = 0.202 \] \[ 2 \times 0.313 = 0.626 \] \[ 3 \times 0.333 = 0.999 \] Now add these values: \[ E(X) = 0 + 0.202 + 0.626 + 0.999 = 1.827 \] The average number of smartphones in a U.S. household is 1.827.