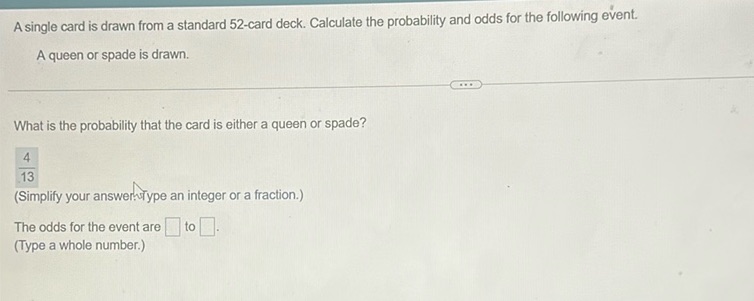
Question: A single card is drawn from a standard 52-card deck. Calculate the probability and odds for the…

A single card is drawn from a standard 52-card deck. Calculate the probability and odds for the following event. A queen or spade is drawn. … What is the probability that the card is either a queen or spade? 4 13 (Simplify your answer. Type an integer or a fraction.) The odds for the event are to . (Type a whole number.)

Solution

To find the probability that the card drawn is either a queen or a spade, we need to consider the total number of favorable outcomes over the total number of possible outcomes in a standard 52-card deck. 1. Identify the total possible outcomes: The total number of cards in the deck is 52. \[ 52 \] 2. Identify the favorable outcomes for either a queen or a spade: - There are 4 queens in the deck (one from each suit). - There are 13 spades in the deck. 3. Consider overlap: The queen of spades is counted in both the number of queens and the number of spades, so we must subtract 1 to avoid double counting. Total favorable outcomes: \[ 4 \ (\text{queens}) + 13 \ (\text{spades}) - 1 \ (\text{queen of spades}) = 16 \] 4. Calculate the probability: \[ \text{Probability} = \frac{\text{Number of favorable outcomes}}{\text{Total possible outcomes}} = \frac{16}{52} \] 5. Simplify the fraction: \[ \frac{16}{52} = \frac{4}{13} \] So, the probability that the card drawn is either a queen or a spade is \(\frac{4}{13}\). 6. Calculate the odds of the event: Odds in favor of the event is the ratio of favorable outcomes to unfavorable outcomes. The number of unfavorable outcomes is the total number of cards minus the number of favorable outcomes: \[ 52 - 16 = 36 \] Therefore, the odds are: \[ \frac{16}{36} = \frac{4}{9} \] So, the odds are \(4\) to \(9\).