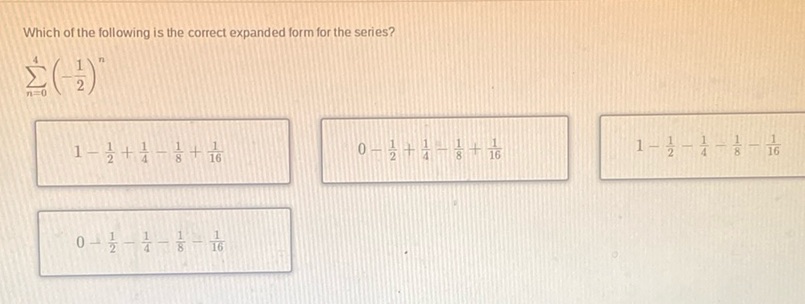
Question: Which of the following is the correct expanded form for the series? \[ \sum_{n=0}^{4} \left(…

Which of the following is the correct expanded form for the series?

\[ \sum_{n=0}^{4} \left( -\frac{1}{2} \right)^n \]

1. \(1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + \frac{1}{16}\)

2. \(0 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + \frac{1}{16}\)

3. \(1 - \frac{1}{2} - \frac{1}{4} - \frac{1}{8} - \frac{1}{16}\)

4. \(0 - \frac{1}{2} - \frac{1}{4} - \frac{1}{8} - \frac{1}{16}\)

Solution

To find the correct expanded form for the series \[ \sum_{n=0}^{4} \left( \frac{1}{2} \right)^n \] we need to calculate each term from \(n=0\) to \(n=4\). Start with \(n=0\): \[ \left( \frac{1}{2} \right)^0 = 1 \] Next, for \(n=1\): \[ \left( \frac{1}{2} \right)^1 = \frac{1}{2} \] For \(n=2\): \[ \left( \frac{1}{2} \right)^2 = \frac{1}{4} \] For \(n=3\): \[ \left( \frac{1}{2} \right)^3 = \frac{1}{8} \] Finally, for \(n=4\): \[ \left( \frac{1}{2} \right)^4 = \frac{1}{16} \] Thus, the expanded form of the series is: \[ 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} \] The correct option is the first one: \(1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16}\).