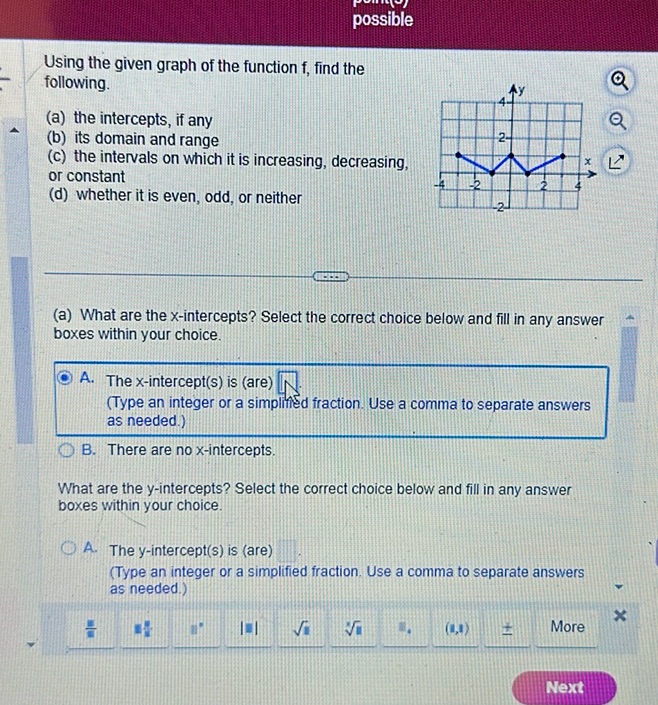
Question: Using the given graph of the function \( f \), find the following. (a) the intercepts, if any…

Using the given graph of the function \( f \), find the following.

(a) the intercepts, if any (b) its domain and range (c) the intervals on which it is increasing, decreasing, or constant (d) whether it is even, odd, or neither

(a) What are the \( x \)-intercepts? Select the correct choice below and fill in any answer boxes within your choice.

A. The \( x \)-intercept(s) is (are) \(\boxed{\quad}\) (Type an integer or a simplified fraction. Use a comma to separate answers as needed.)

B. There are no \( x \)-intercepts.

What are the \( y \)-intercepts? Select the correct choice below and fill in any answer boxes within your choice.

A. The \( y \)-intercept(s) is (are) \(\boxed{\quad}\) (Type an integer or a simplified fraction. Use a comma to separate answers as needed.)

Solution

(a) The x-intercepts are the points where the graph intersects the x-axis. These occur when \( y = 0 \). From the graph, the x-intercepts are at \( x = -2 \) and \( x = 1 \). (b) The domain of the function is the set of all possible x-values. Observing the graph, the domain is all real numbers between \( x = -2 \) and \( x = 2 \). The range of the function is the set of all possible y-values. From the graph, the range is all real numbers between \( y = -2 \) and \( y = 2 \). (c) To find the intervals on which the function is increasing, decreasing, or constant, observe the direction of the graph: - Increasing on: \( (-2, -1) \) and \( (0, 1) \) - Decreasing on: \( (-1, 0) \) and \( (1, 2) \) - Constant on: None (d) A function is even if \( f(x) = f(-x) \) for all x in the domain, and it is odd if \( f(-x) = -f(x) \). By visual inspection, the graph does not show symmetry around the y-axis or the origin. Thus, the function is neither even nor odd.