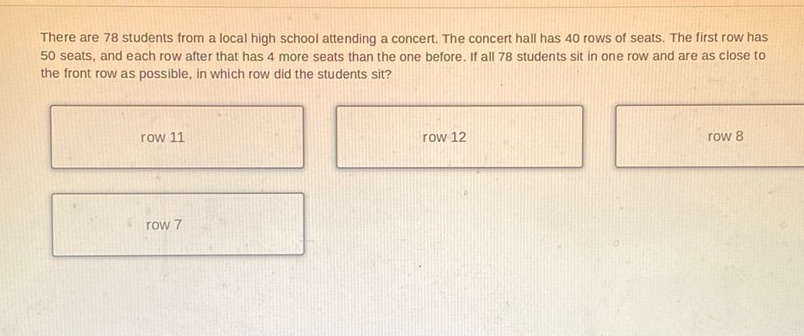
Question: There are 78 students from a local high school attending a concert. The concert hall has 40 rows of…

There are 78 students from a local high school attending a concert. The concert hall has 40 rows of seats. The first row has 50 seats, and each row after that has 4 more seats than the one before. If all 78 students sit in one row and are as close to the front row as possible, in which row did the students sit?

row 11 row 12 row 8 row 7

Solution

To solve the problem, we need to find in which row all 78 students can sit together. The first row has 50 seats. Each subsequent row has 4 more seats than the one before. Let’s express the number of seats in the \(n\)-th row as: \[ \text{Seats in row } n = 50 + 4(n-1) \] We need to find the smallest \(n\) such that \[ 50 + 4(n-1) \geq 78 \] Start by simplifying the equation: \[ 50 + 4n - 4 \geq 78 \] \[ 4n + 46 \geq 78 \] Subtract 46 from both sides: \[ 4n \geq 32 \] Divide by 4: \[ n \geq 8 \] Thus, the smallest row number \(n\) that can accommodate all 78 students is the 8th row. The students sit in row 8.