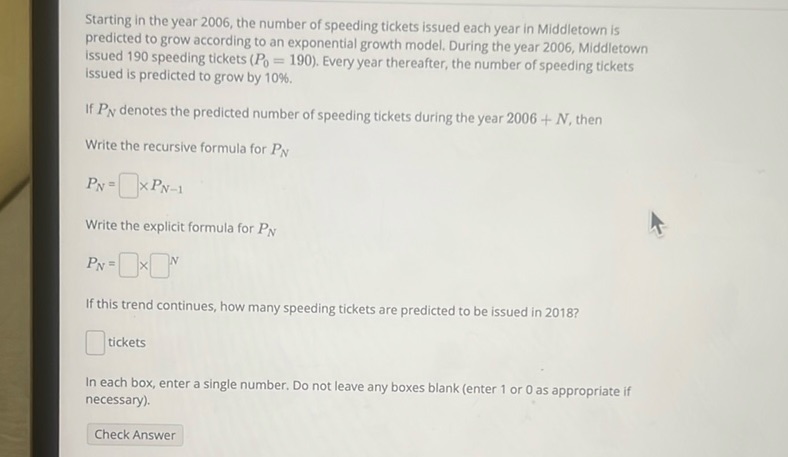
Question: Starting in the year 2006, the number of speeding tickets issued each year in Middletown is…

Starting in the year 2006, the number of speeding tickets issued each year in Middletown is predicted to grow according to an exponential growth model. During the year 2006, Middletown issued 190 speeding tickets ($P_0 = 190$). Every year thereafter, the number of speeding tickets issued is predicted to grow by 10%.

If $P_N$ denotes the predicted number of speeding tickets during the year $2006 + N$, then

Write the recursive formula for $P_N$

$P_N = \boxed{\phantom{0}} \times P_{N-1}$

Write the explicit formula for $P_N$

$P_N = \boxed{\phantom{0}} \times \boxed{\phantom{0}}^N$

If this trend continues, how many speeding tickets are predicted to be issued in 2018?

$\boxed{\phantom{0}}$ tickets

In each box, enter a single number. Do not leave any boxes blank (enter 1 or 0 as appropriate if necessary).

Check Answer

Solution

First, let’s establish the recursive formula for \( P_N \): \[ P_N = 1.10 \times P_{N-1} \] Next, we’ll derive the explicit formula for \( P_N \): \[ P_N = 190 \times 1.10^N \] Finally, to predict the number of speeding tickets in 2018, we calculate \( P_{12} \) (since 2018 is 12 years after 2006): \[ P_{12} = 190 \times 1.10^{12} \approx 596 \text{ tickets} \]