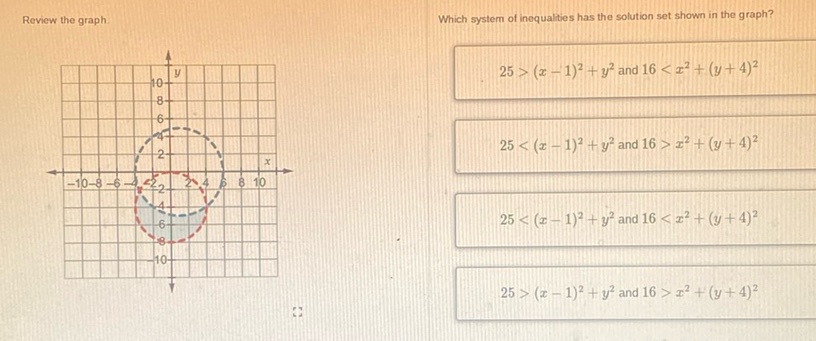
Question: Review the graph. Which system of inequalities has the solution set shown in the graph? \[…

Review the graph.

Which system of inequalities has the solution set shown in the graph?

\[ \begin{array}{|c|} \hline 25 > (x - 1)^2 + y^2 \text{ and } 16 < x^2 + (y + 4)^2 \\ \hline 25 < (x - 1)^2 + y^2 \text{ and } 16 > x^2 + (y + 4)^2 \\ \hline 25 < (x - 1)^2 + y^2 \text{ and } 16 < x^2 + (y + 4)^2 \\ \hline 25 > (x - 1)^2 + y^2 \text{ and } 16 > x^2 + (y + 4)^2 \\ \hline \end{array} \]

Solution

The graph shows two circles with a shaded intersection area. We need to determine which system of inequalities correctly represents this area. The inequalities describe circles. Here’s how you break it down: 1. The first inequality \(25 > (x-1)^2 + y^2\) represents a circle with center at \((1, 0)\) and radius 5. 2. The second inequality \(16 < x^2 + (y+4)^2\) represents the region outside a circle with center at \((0, -4)\) and radius 4. The solution set is the area inside the first circle and outside the second circle. This matches with the graph where the overlapping region is in the upper right of the smaller circle and outside the larger circle. Thus, the correct answer is: \[ \begin{cases} 25 > (x-1)^2 + y^2 & \\ 16 < x^2 + (y+4)^2 & \end{cases} \]