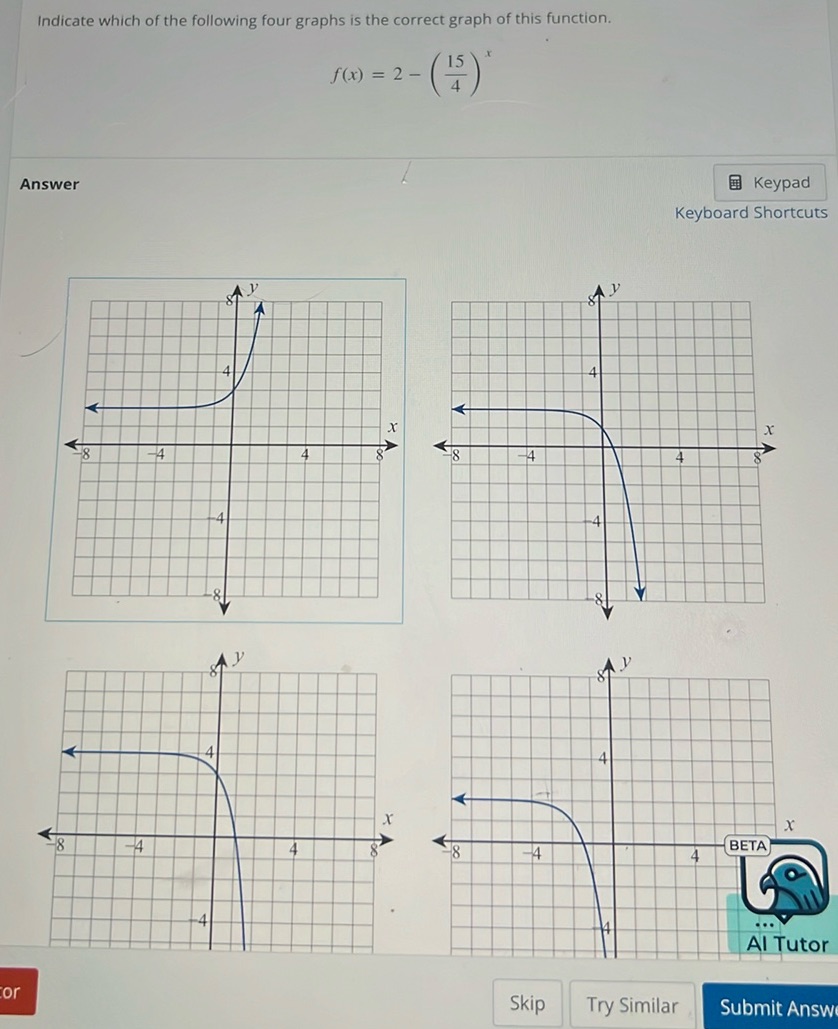
Question: Indicate which of the following four graphs is the correct graph of this function. \[ f(x) = 2 -…

Indicate which of the following four graphs is the correct graph of this function.

\[ f(x) = 2 - \left( \frac{15}{4} \right)^x \]

Answer

[Graphs are shown, but not transcribed as they are visual representations.]

Keypad

Keyboard Shortcuts

Submit Answer

Solution

To solve this problem, we need to analyze the given function: \[ f(x) = 2 - \left(\frac{15}{4}\right)^x \] This function is an exponential function, where the base \(\frac{15}{4}\) is greater than 1. Exponential functions with bases greater than 1 exhibit the following characteristics: 1. The graph increases from left to right. 2. The horizontal asymptote is typically the constant term, which in this case is \(y = 2\). 3. As \(x\) approaches positive infinity, the function will increase rapidly. 4. As \(x\) approaches negative infinity, the function will approach the horizontal asymptote from below. Based on these properties, the correct graph will be: - Approaching \(y = 2\) as a horizontal asymptote. - Rising from left to right. Among the four graphs shown, the correct graph is the one in the first position (top left), as it starts below the asymptote and rises as it moves to the right.