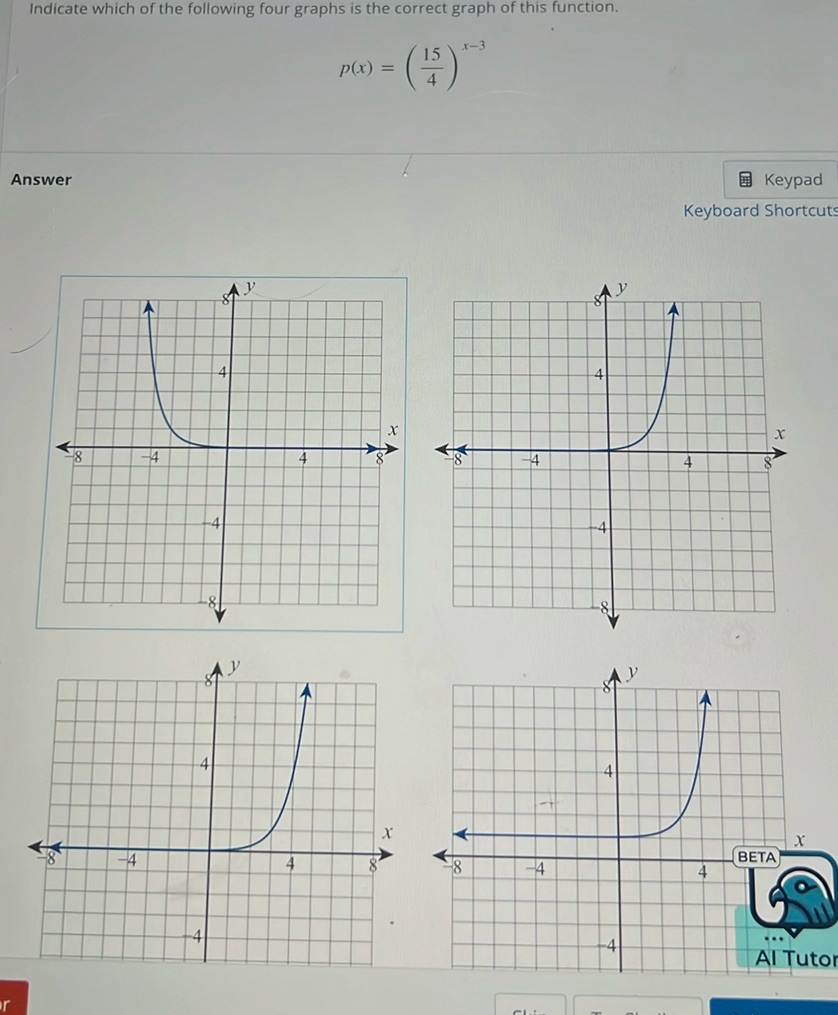
Question: Indicate which of the following four graphs is the correct graph of this function. \[ p(x) =…

Indicate which of the following four graphs is the correct graph of this function.

\[ p(x) = \left( \frac{15}{4} \right)^{x-3} \]

Answer

[Four graphs are shown, but the specific details of the graphs are not transcribed here.]

Solution

To solve this problem, we’ll analyze the function \( p(x) = \left( \frac{15}{4} \right)^{x-3} \). The function is an exponential function of the form \( a^{x-h} \), where \( a = \frac{15}{4} \) and \( h = 3 \). 1. Since \( a > 1 \), the exponential function is increasing. 2. The horizontal shift is determined by \( h = 3 \). This means the basic graph \( y = a^x \) is shifted 3 units to the right. 3. The graph should have the point \( (3, 1) \) since when \( x = 3 \), \( p(x) = \left( \frac{15}{4} \right)^0 = 1 \). 4. The function grows without bound as \( x \to \infty \) and approaches zero as \( x \to -\infty \). Upon examining the four graphs, the top right graph correctly shows an increasing exponential function shifted to the right, which matches the behavior described above.