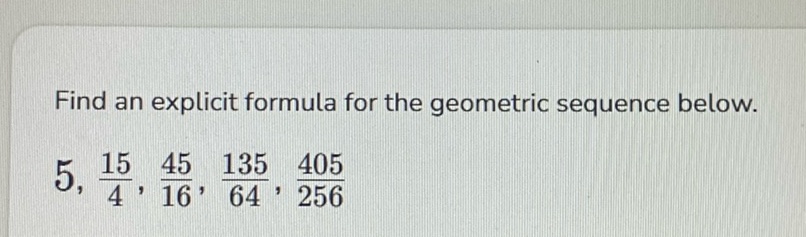
Question: Find an explicit formula for the geometric sequence below. \[ 5, \frac{15}{4}, \frac{45}{16},…

Find an explicit formula for the geometric sequence below.

\[ 5, \frac{15}{4}, \frac{45}{16}, \frac{135}{64}, \frac{405}{256} \]

Solution

To find the explicit formula for the given geometric sequence, we can use the general formula for a geometric sequence: \[ a_n = a_1 \cdot r^{n-1} \] where \( a_1 \) is the first term and \( r \) is the common ratio. First, identify the first term: The first term \( a_1 = 5 \). Next, find the common ratio \( r \) by dividing the second term by the first term: \[ r = \frac{\frac{15}{4}}{5} = \frac{15}{4} \times \frac{1}{5} = \frac{3}{4} \] Now that we have \( a_1 = 5 \) and \( r = \frac{3}{4} \), we can write the explicit formula for the geometric sequence: \[ a_n = 5 \cdot \left( \frac{3}{4} \right)^{n-1} \] This formula represents the explicit formula for the given geometric sequence.