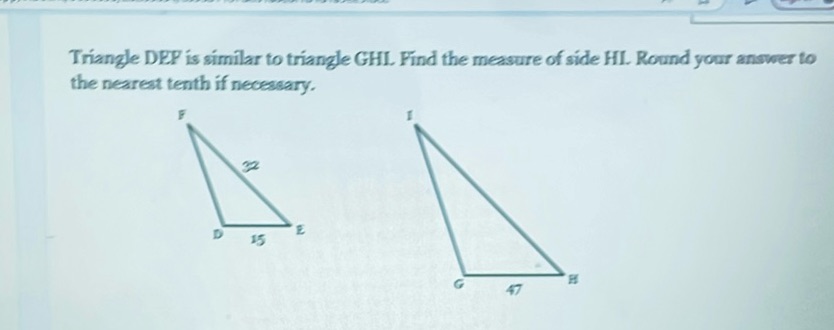
Question: Triangle DEF is similar to triangle GHI. Find the measure of side HI. Round your answer to the…

Triangle DEF is similar to triangle GHI. Find the measure of side HI. Round your answer to the nearest tenth if necessary.

[Diagram of two similar triangles, DEF and GHI, with side lengths labeled as follows:

• Triangle DEF: DE = 15, EF = 32
• Triangle GHI: GH = 47, HI = ?]

Solution

To solve the problem, use the property that similar triangles have proportional sides. Given triangles \(\triangle DEF \sim \triangle GHI\): 1. Set up the proportion using known side lengths: \[ \frac{DE}{GH} = \frac{EF}{HI} \] 2. Substitute the known values into the proportion: \[ \frac{15}{47} = \frac{22}{HI} \] 3. Solve for \(HI\): \[ 15 \cdot HI = 22 \cdot 47 \] 4. Calculate \(22 \cdot 47\): \[ 22 \cdot 47 = 1034 \] 5. Divide both sides by 15 to find \(HI\): \[ HI = \frac{1034}{15} \] 6. Calculate \(\frac{1034}{15}\): \[ HI \approx 68.9333 \] 7. Round to the nearest tenth as instructed: \[ HI \approx 68.9 \] Thus, the measure of side \(HI\) is approximately 68.9.