Question: Question Progress Homework Progress 18 / 26 Marks 50% ABCF is a rectangle. CDEF is a trapezium…

Question Progress

Homework Progress 18 / 26 Marks 50%

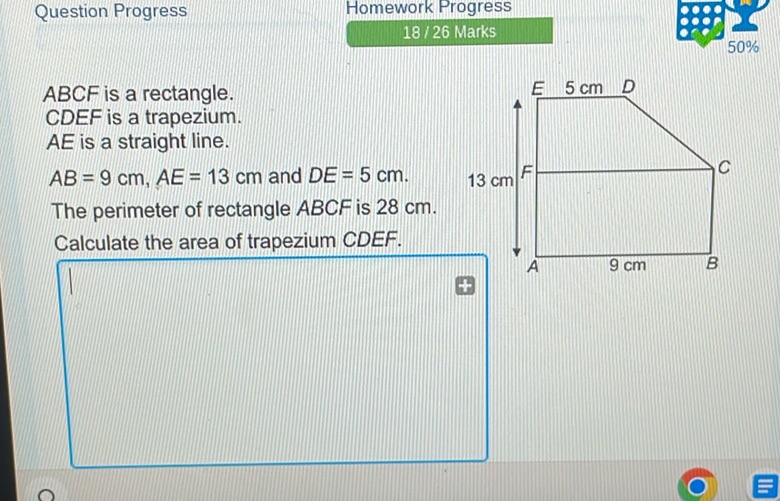
ABCF is a rectangle. CDEF is a trapezium. AE is a straight line.

AB = 9 cm, AE = 13 cm and DE = 5 cm. The perimeter of rectangle ABCF is 28 cm. Calculate the area of trapezium CDEF.

[Diagram of a rectangle ABCF and a trapezium CDEF with dimensions labeled]

[Answer box]

Solution

To solve the problem of finding the area of trapezium \( CDEF \), we’ll follow these steps: First, we determine the dimensions of rectangle \( ABCF \). \[ \text{Perimeter of rectangle } ABCF = 2(AB + BC) = 28 \text{ cm} \\ 2(9 \text{ cm} + BC) = 28 \text{ cm} \\ 18 \text{ cm} + 2BC = 28 \text{ cm} \\ 2BC = 10 \text{ cm} \\ BC = 5 \text{ cm} & \] Next, we analyze the trapezium \( CDEF \). \[ \text{Given: } DE = 5 \text{ cm}, \ AE = 13 \text{ cm} & \] Since \( AE \) is a straight line and \( ABCF \) is a rectangle, we can consider triangle \( ADE \). \[ \text{Using the Pythagorean theorem in } \triangle ADE: \\ AD^2 + DE^2 = AE^2 \\ AD^2 + 5^2 = 13^2 \\ AD^2 + 25 = 169 \\ AD^2 = 144 \\ AD = 12 \text{ cm} & \] Now, \( AD \) represents the height of trapezium \( CDEF \). \[ \text{Height of trapezium } h = AD = 12 \text{ cm} & \] The bases of trapezium \( CDEF \) are \( CD \) and \( EF \). Since \( ABCF \) is a rectangle, \( CD = AB = 9 \text{ cm} \), and \( EF = DE = 5 \text{ cm} \). \[ \text{Base } CD = 9 \text{ cm}, \ \text{Base } EF = 5 \text{ cm} & \] Finally, we calculate the area of trapezium \( CDEF \). \[ \text{Area} = \frac{1}{2} \times (CD + EF) \times h \\ = \frac{1}{2} \times (9 \text{ cm} + 5 \text{ cm}) \times 12 \text{ cm} \\ = \frac{1}{2} \times 14 \text{ cm} \times 12 \text{ cm} \\ = 7 \text{ cm} \times 12 \text{ cm} \\ = 84 \text{ cm}^2 & \] Answer: The area of trapezium \( CDEF \) is \( 84 \text{ cm}^2 \).