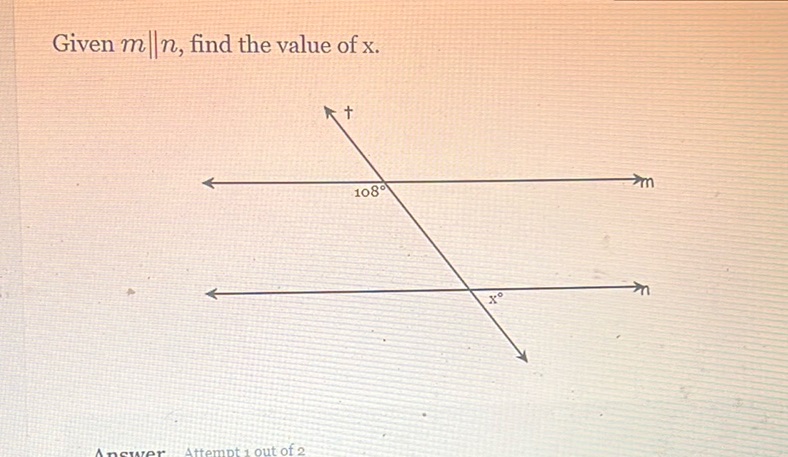
Question: Given \( m \parallel n \), find the value of \( x \). [Diagram: Two parallel lines \( m \)…

Given \( m \parallel n \), find the value of \( x \).

[Diagram: Two parallel lines \( m \) and \( n \) are intersected by a transversal. One angle is labeled \( 108^\circ \), and the other angle is labeled \( x^\circ \).]

Solution

Given that lines \( m \) and \( n \) are parallel, the angles formed by a transversal cutting through these lines allow us to use the property of corresponding angles. In this case, the given angle \( 108^\circ \) is supplementary to angle \( x^\circ \) because they are on a straight line. According to the supplementary angle theorem, the angles on a straight line add up to \( 180^\circ \). So, we have: \[ x + 108 = 180 \] Subtract \( 108 \) from both sides: \[ x = 180 - 108 \] Simplify the equation: \[ x = 72 \] Therefore, the value of \( x \) is \( 72^\circ \).