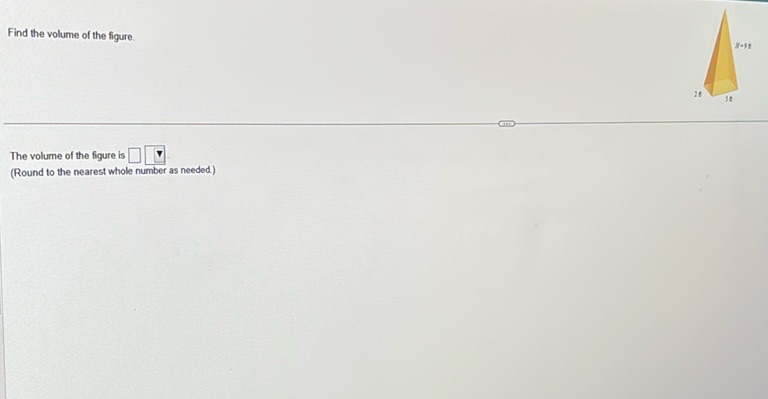
Question: Find the volume of the figure. The volume of the figure is \(\boxed{\phantom{0}}\) (Round to…

Find the volume of the figure.

The volume of the figure is \(\boxed{\phantom{0}}\) (Round to the nearest whole number as needed.)

[Image of a triangular prism with dimensions labeled: 28, 16, and 20]

Solution

To find the volume of a triangular pyramid (also known as a tetrahedron), we use the formula: \[ V = \frac{1}{3} \times B \times h \] where \( B \) is the area of the base and \( h \) is the height of the pyramid. Identify the dimensions from the image: - The base of the triangular pyramid is 7 units. - The height from the base to the apex is 11 units. - The base’s height of the triangle is 3 units (perpendicular to the base of the triangle). Find the area of the triangular base: \[ B = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 7 \times 3 = 10.5 \] Now, use the volume formula: \[ V = \frac{1}{3} \times 10.5 \times 11 \] \[ V = \frac{1}{3} \times 115.5 \] \[ V = 38.5 \] Since the problem asks to round to the nearest whole number, the volume of the pyramid is \( 39 \) cubic units.