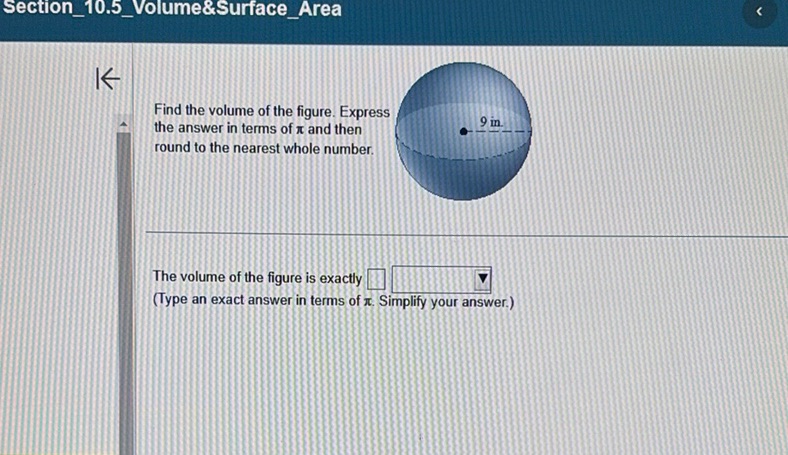
Question: Find the volume of the figure. Express the answer in terms of π and then round to the nearest whole…

Find the volume of the figure. Express the answer in terms of π and then round to the nearest whole number.

[Image of a sphere with a radius of 9 in.]

The volume of the figure is exactly \(\boxed{\phantom{0}}\) (Type an exact answer in terms of π. Simplify your answer.)

Solution

The problem asks to find the volume of a sphere with a radius of 9 meters, expressed in terms of \(\pi\) and then rounded to the nearest whole number. First, recall the formula for the volume of a sphere: \[ V = \frac{4}{3} \pi r^3 \] Substitute the radius \(r = 9\) meters into the formula: \[ V = \frac{4}{3} \pi (9)^3 \] Calculate \(9^3\): \[ 9^3 = 729 \] Now substitute back into the volume formula: \[ V = \frac{4}{3} \pi \times 729 \] Simplify the expression: \[ V = \frac{4 \times 729}{3} \pi \] Calculate \(4 \times 729\): \[ 4 \times 729 = 2916 \] Divide by 3: \[ V = \frac{2916}{3} \pi \] \[ V = 972 \pi \] Thus, the volume of the sphere in terms of \(\pi\) is \(972 \pi\). For the approximate volume, use \(\pi \approx 3.14159\): \[ V \approx 972 \times 3.14159 \] Calculate the approximation: \[ V \approx 3056.99 \] Round to the nearest whole number: \[ V \approx 3057 \] So, the volume of the sphere is exactly \(972 \pi\) and approximately 3057 cubic meters.