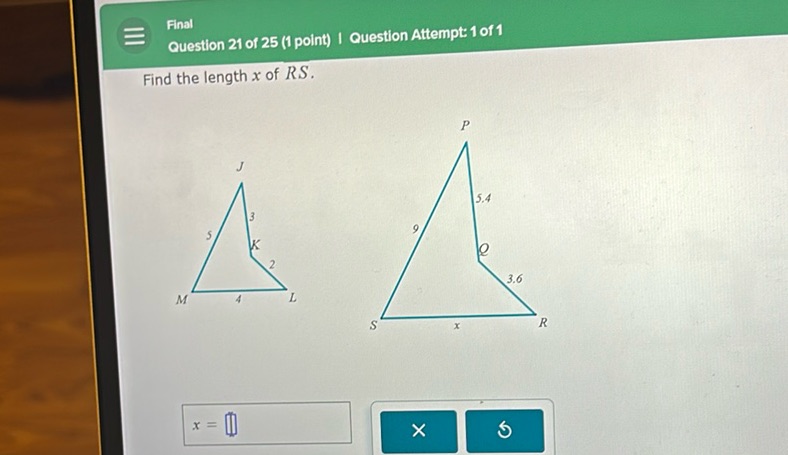
Question: Find the length x of RS.

Solution

To find the length \( x \) of \( RS \), we can use the concept of similar triangles. The triangles \( \triangle JKL \) and \( \triangle PQR \) are similar because their corresponding angles are equal. The side lengths of similar triangles are proportional. Therefore, we can set up a proportion between the corresponding sides of the triangles: \[ \frac{JK}{PQ} = \frac{KL}{QR} = \frac{JL}{PR} \] Given: \( JK = 3 \), \( KL = 2 \), \( JL = 5 \) \( PQ = 5.4 \), \( QR = 3.6 \), \( PR = 9 \) Let’s find \( x \) using the proportion between \( KL \) and \( QR \): \[ \frac{KL}{QR} = \frac{JL}{PR} \] \[ \frac{2}{3.6} = \frac{5}{x} \] Cross multiply to solve for \( x \): \[ 2x = 5 \times 3.6 \] \[ 2x = 18 \] Divide both sides by 2: \[ x = 9 \] The length of \( RS \) is \( 9 \).