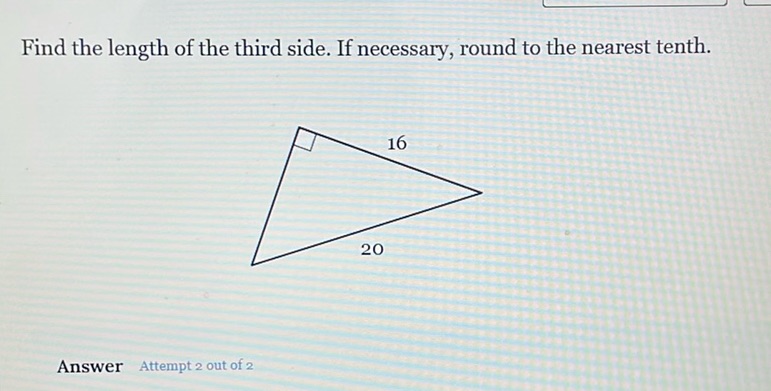
Question: Find the length of the third side. If necessary, round to the nearest tenth. [Image of a right…

Find the length of the third side. If necessary, round to the nearest tenth.

[Image of a right triangle with sides labeled 16 and 20]

Answer

Solution

To find the length of the third side in a right-angled triangle, we can use the Pythagorean theorem, which is: \[ c^2 = a^2 + b^2 \] where \( c \) is the hypotenuse and \( a \) and \( b \) are the other two sides. Given \( a = 16 \) and \( c = 20 \), we need to find \( b \). First, substitute the known values into the equation: \[ 20^2 = 16^2 + b^2 \] Calculate the squares: \[ 400 = 256 + b^2 \] Subtract 256 from both sides to solve for \( b^2 \): \[ 400 - 256 = b^2 \] \[ 144 = b^2 \] Take the square root of both sides to find \( b \): \[ b = \sqrt{144} \] \[ b = 12 \] So, the length of the third side is 12.