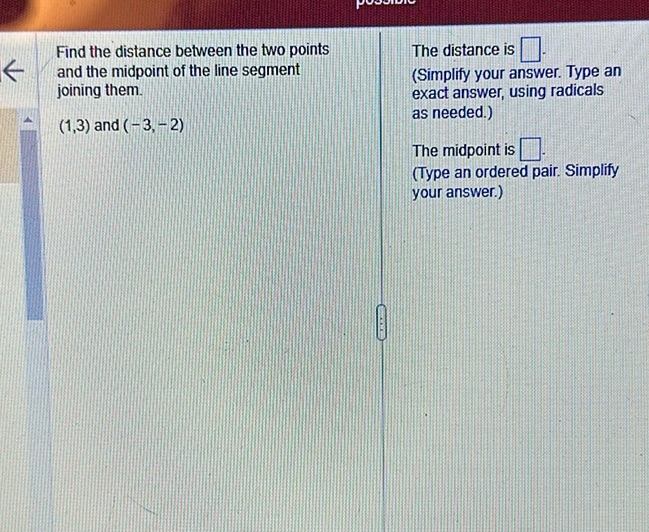
Question: Find the distance between the two points and the midpoint of the line segment joining them. (1, 3)…

Find the distance between the two points and the midpoint of the line segment joining them.

(1, 3) and (-3, -2)

The distance is \(\boxed{\phantom{}}\).

(Simplify your answer. Type an exact answer, using radicals as needed.)

The midpoint is \(\boxed{\phantom{}}\).

(Type an ordered pair. Simplify your answer.)

Solution

To solve the problem, we need to find the distance between the two points and the midpoint of the line segment joining them. ### Points The points given are \((1, 3)\) and \((-3, -2)\). ### Distance Formula To find the distance between the two points \((x_1, y_1)\) and \((x_2, y_2)\), use the distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \] Substitute \((x_1, y_1) = (1, 3)\) and \((x_2, y_2) = (-3, -2)\): \[ d = \sqrt{(-3 - 1)^2 + (-2 - 3)^2} \] \[ d = \sqrt{(-4)^2 + (-5)^2} \] \[ d = \sqrt{16 + 25} \] \[ d = \sqrt{41} \] The distance is \(\sqrt{41}\). ### Midpoint Formula The midpoint \((x_m, y_m)\) of the segment joining \((x_1, y_1)\) and \((x_2, y_2)\) is given by: \[ (x_m, y_m) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) \] Substitute \((x_1, y_1) = (1, 3)\) and \((x_2, y_2) = (-3, -2)\): \[ (x_m, y_m) = \left(\frac{1 + (-3)}{2}, \frac{3 + (-2)}{2}\right) \] \[ (x_m, y_m) = \left(\frac{-2}{2}, \frac{1}{2}\right) \] \[ (x_m, y_m) = (-1, 0.5) \] The midpoint is \((-1, 0.5)\).