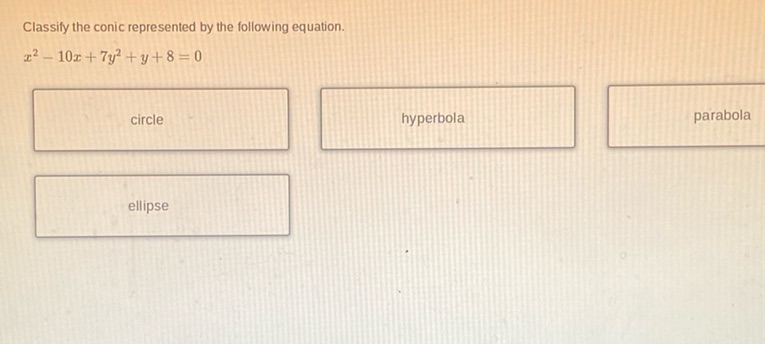
Question: Classify the conic represented by the following equation. \[ x^2 - 10x + 7y^2 + y + 8 = 0 \]…

Classify the conic represented by the following equation.

\[ x^2 - 10x + 7y^2 + y + 8 = 0 \]

circle hyperbola parabola ellipse

Solution

To classify the conic section represented by the equation \[ x^2 - 10x + 7y^2 + y + 8 = 0 \] we observe the coefficients of \(x^2\) and \(y^2\). Given equation: \[ x^2 - 10x + 7y^2 + y + 8 = 0 \] Identify coefficients of \(x^2\) and \(y^2\): \[ A = 1, \quad C = 7 \] Since \(A\) and \(C\) are both positive and \(A \neq C\), the conic section is an ellipse.