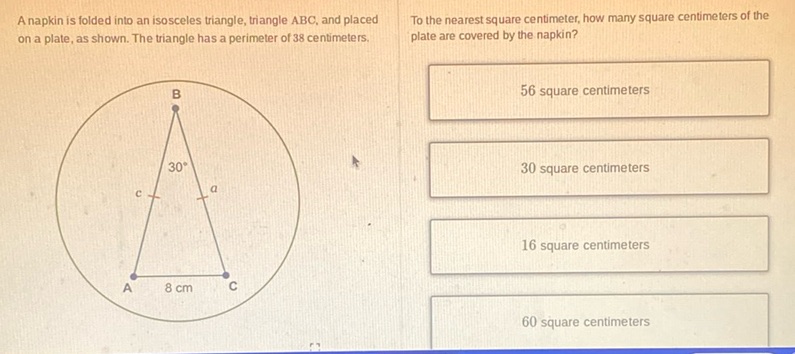
Question: A napkin is folded into an isosceles triangle, triangle ABC, and placed on a plate, as shown. The…

A napkin is folded into an isosceles triangle, triangle ABC, and placed on a plate, as shown. The triangle has a perimeter of 38 centimeters.

[Diagram of an isosceles triangle ABC with a 30° angle at vertex B and side AC labeled as 8 cm]

To the nearest square centimeter, how many square centimeters of the plate are covered by the napkin?

• 56 square centimeters
• 30 square centimeters
• 16 square centimeters
• 60 square centimeters

Solution

To solve the problem, follow these steps: 1. Identify the given information: - The triangle is isosceles with sides \(AB = AC = a\) and base \(BC = 8\). - The perimeter of the triangle is 38 cm. 2. Set up the equation for the perimeter: \[ a + a + 8 = 38 \] 3. Solve for \(a\): \[ 2a + 8 = 38 \] Subtract 8 from both sides: \[ 2a = 30 \] Divide by 2: \[ a = 15 \] 4. Use the area formula for a triangle: - For an isosceles triangle with angle \(\theta\) and equal sides \(a\), \( \text{Area} = \frac{1}{2} ab \sin C \). - In this case, \(\theta = 30^\circ\), \(a = 15\), and the base \(b = 8\). 5. Substitute into the area formula: \[ \text{Area} = \frac{1}{2} \times 8 \times 15 \times \sin 30^\circ \] \(\sin 30^\circ = \frac{1}{2}\): \[ \text{Area} = \frac{1}{2} \times 8 \times 15 \times \frac{1}{2} \] 6. Calculate the area: \[ \text{Area} = 4 \times 15 \times \frac{1}{2} = 30 \] Thus, the area of the plate covered by the napkin is 30 square centimeters.