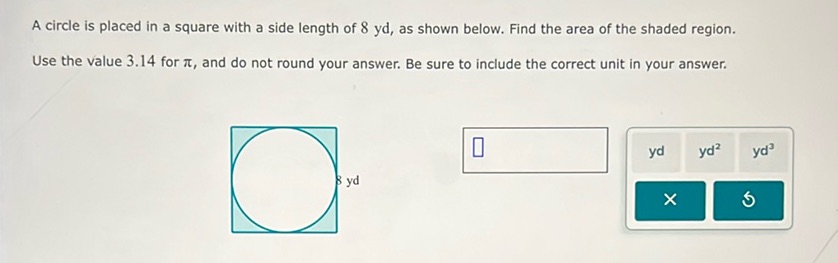
Question: A circle is placed in a square with a side length of 8 yd, as shown below. Find the area of the…

A circle is placed in a square with a side length of 8 yd, as shown below. Find the area of the shaded region.

Use the value 3.14 for $\pi$, and do not round your answer. Be sure to include the correct unit in your answer.

[Diagram of a square with a circle inscribed in it, side length of the square is 8 yd]

[Answer box for the area of the shaded region]

[Units: yd, yd², yd³]

[Buttons: ×, ÷]

Solution

Step 1: Calculate the area of the square. \[ \text{Area}{\text{square}} = \text{side}^2 = 8^2 = 64 \, \text{yd}^2 \] Step 2: Determine the radius of the inscribed circle. \[ \text{radius} = \frac{\text{side}}{2} = \frac{8}{2} = 4 \, \text{yd} \] Step 3: Calculate the area of the circle. \[ \text{Area}{\text{circle}} = \pi r^2 = 3.14 \times 4^2 = 3.14 \times 16 = 50.24 \, \text{yd}^2 \] Step 4: Find the area of the shaded region. \[ \text{Area}{\text{shaded}} = \text{Area}{\text{square}} - \text{Area}_{\text{circle}} = 64 \, \text{yd}^2 - 50.24 \, \text{yd}^2 = 13.76 \, \text{yd}^2 \] The area of the shaded region is 13.76 yd².