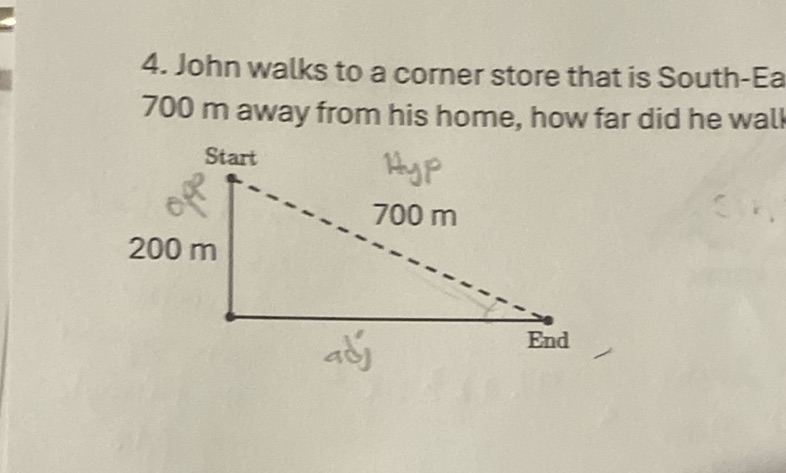
Question: 4. John walks to a corner store that is South-East 700 m away from his home, how far did he walk?…

4. John walks to a corner store that is South-East 700 m away from his home, how far did he walk?

\[ \text{Start} \quad \text{Hyp} \quad \text{700 m} \]

\[ \text{200 m} \]

\[ \text{End} \]

Solution

To solve the problem, we need to figure out how far John walked in total. The problem describes a right triangle where: - The hypotenuse is 700 m. - One leg (opposite) is 200 m. We are solving for the other leg (adjacent), which represents part of John’s walk. Using the Pythagorean theorem: \[ c^2 = a^2 + b^2 \] where \( c \) is the hypotenuse, \( a \) is one leg, and \( b \) is the other leg. Substitute the known values: \[ 700^2 = 200^2 + b^2 \] Calculate \( 700^2 \): \[ 490000 = 40000 + b^2 \] Subtract 40000 from both sides to solve for \( b^2 \): \[ 490000 - 40000 = b^2 \] \[ 450000 = b^2 \] Take the square root of both sides to solve for \( b \): \[ b = \sqrt{450000} \] Calculate \( b \): \[ b = 670.82 \, (\text{approximately}) \] Thus, the total distance John walked is: \[ 200 + 670.82 = 870.82 \, \text{meters} \] So, John walked approximately 870.82 meters.