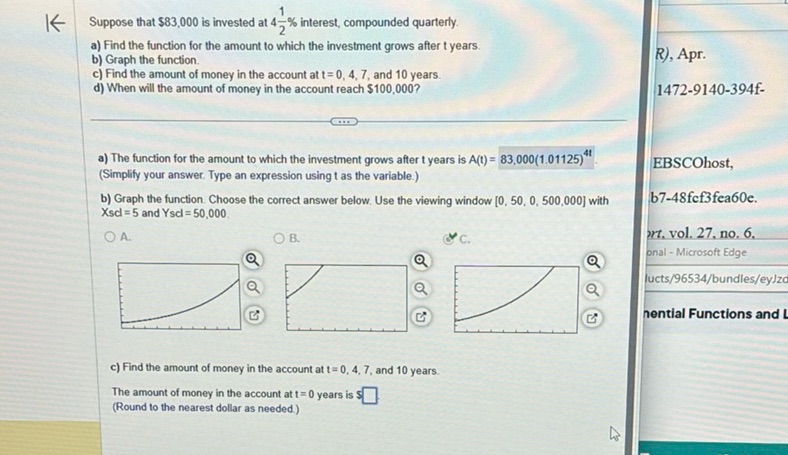
Question: Suppose that $83,000 is invested at 4\frac{1}{2}\%$ interest, compounded quarterly. a) Find the…

Suppose that $83,000 is invested at 4\frac{1}{2}\%$ interest, compounded quarterly.

a) Find the function for the amount to which the investment grows after t years.

b) Graph the function.

c) Find the amount of money in the account at t = 0, 4, 7, and 10 years.

d) When will the amount of money in the account reach $100,000?

a) The function for the amount to which the investment grows after t years is A(t) = 83,000(1.01125)^{4t}.

(Simplify your answer. Type an expression using t as the variable.)

b) Graph the function. Choose the correct answer below. Use the viewing window [0, 50, 0, 500,000] with XscI = 5 and YscI = 50,000.

c) Find the amount of money in the account at t = 0, 4, 7, and 10 years.

The amount of money in the account at t = 0 years is $____.

(Round to the nearest dollar as needed.)

Solution

a) The function for the amount to which the investment grows after \( t \) years is given by the formula for compound interest: \[ A(t) = P \left(1 + \frac{r}{n}\right)^{nt} \] Here, \( P = 83,000 \), \( r = 0.0425 \), and \( n = 4 \) (because the interest is compounded quarterly). \[ A(t) = 83,000 \left(1 + \frac{0.0425}{4}\right)^{4t} = 83,000 (1.010625)^{4t} \] b) The correct graph of this function is option C, which shows exponential growth. c) Find the amount of money in the account at \( t = 0, 4, 7, \) and \( 10 \) years. For \( t = 0 \): \[ A(0) = 83,000 (1.010625)^{4 \times 0} = 83,000 \times 1 = 83,000 \] For \( t = 4 \): \[ A(4) = 83,000 (1.010625)^{16} \] Calculating: \[ A(4) \approx 83,000 \times 1.18515 = 98,366 \] For \( t = 7 \): \[ A(7) = 83,000 (1.010625)^{28} \] Calculating: \[ A(7) \approx 83,000 \times 1.32055 = 109,605 \] For \( t = 10 \): \[ A(10) = 83,000 (1.010625)^{40} \] Calculating: \[ A(10) \approx 83,000 \times 1.47201 = 122,177 \] d) To find when the amount will reach $100,000, solve: \[ 100,000 = 83,000 (1.010625)^{4t} \] Dividing both sides by 83,000: \[ 1.20482 = (1.010625)^{4t} \] Take the natural logarithm of both sides: \[ \ln(1.20482) = 4t \ln(1.010625) \] Solve for \( t \): \[ t = \frac{\ln(1.20482)}{4 \ln(1.010625)} \approx 4.945 \text{ years} \] Thus, it will take approximately \( 4.95 \) years for the investment to reach $100,000.