Published
- 1 min read
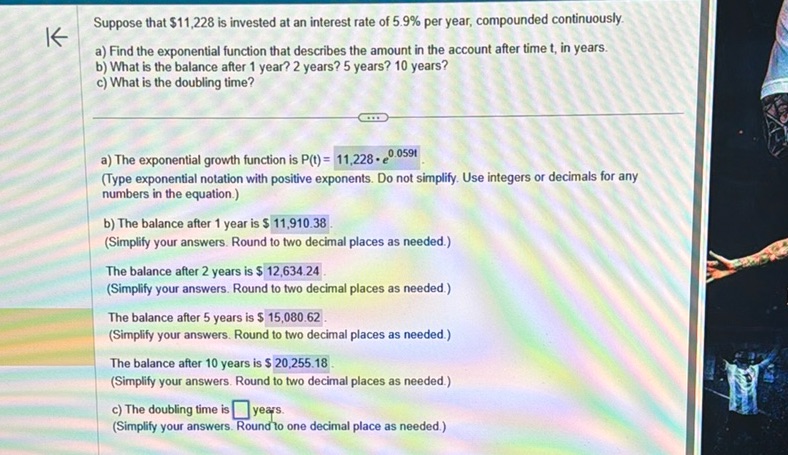
Question: Suppose that $11,228 is invested at an interest rate of 5.9% per year, compounded continuously. a)…
Suppose that $11,228 is invested at an interest rate of 5.9% per year, compounded continuously.
a) Find the exponential function that describes the amount in the account after time t, in years.
b) What is the balance after 1 year? 2 years? 5 years? 10 years?
c) What is the doubling time?
a) The exponential growth function is P(t) = 11,228 * e^(0.059t).
b) The balance after 1 year is $11,910.38.
The balance after 2 years is $12,634.24.
The balance after 5 years is $15,080.62.
The balance after 10 years is $20,255.18.
c) The doubling time is 12 years.
Solution
a) The exponential growth function for continuous compounding is given by: \[ P(t) = P_0 e^{rt} \] where \( P_0 = 11,228 \) is the initial investment, \( r = 0.059 \) is the rate, and \( t \)

