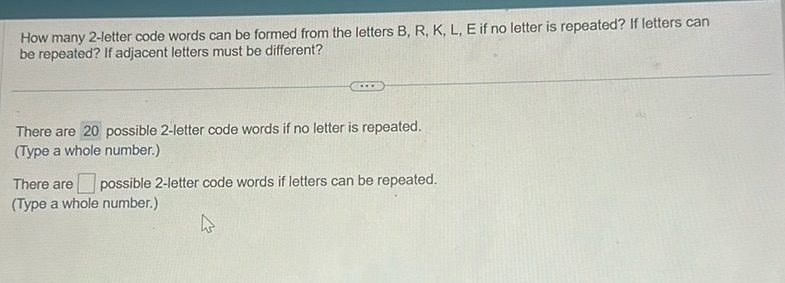
Question: How many 2-letter code words can be formed from the letters B, R, K, L, E if no letter is repeated?…

How many 2-letter code words can be formed from the letters B, R, K, L, E if no letter is repeated? If letters can be repeated? If adjacent letters must be different? … There are 20 possible 2-letter code words if no letter is repeated. (Type a whole number.) There are possible 2-letter code words if letters can be repeated. (Type a whole number.)

Solution

To find the number of possible 2-letter code words if letters can be repeated but adjacent letters must be different, we follow these steps: The letters available are B, R, K, L, and E. First, calculate the number of choices for the first letter. There are 5 letters, so there are 5 choices for the first letter. For the second letter, since it has to be different from the first letter, there are 4 remaining choices. The total number of possible 2-letter code words is the product of the choices for each position: \[ 5 \times 4 = 20 \] So, there are 20 possible 2-letter code words if letters can be repeated but adjacent letters must be different.