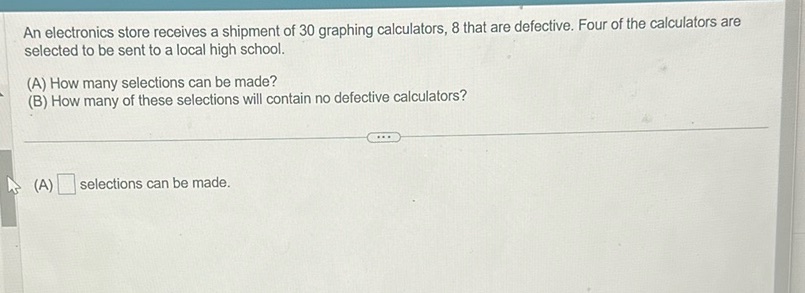
Question: An electronics store receives a shipment of 30 graphing calculators, 8 that are defective. Four of…

An electronics store receives a shipment of 30 graphing calculators, 8 that are defective. Four of the calculators are selected to be sent to a local high school. (A) How many selections can be made? (B) How many of these selections will contain no defective calculators? (A) selections can be made.

Solution

To solve the problem, we need to use combinations. (A) Calculate the number of ways to select 4 calculators from 30. The number of combinations is given by: \[ \binom{30}{4} = \frac{30 \times 29 \times 28 \times 27}{4 \times 3 \times 2 \times 1} \] Calculating the value, we get: \[ \binom{30}{4} = 27{405} \] So, 27,405 selections can be made. (B) Calculate the number of selections that contain no defective calculators. First, determine the number of non-defective calculators. There are: \[ 30 - 8 = 22 \] Now, calculate the combinations of selecting 4 calculators from these 22 non-defective calculators: \[ \binom{22}{4} = \frac{22 \times 21 \times 20 \times 19}{4 \times 3 \times 2 \times 1} \] Calculating the value, we get: \[ \binom{22}{4} = 7{315} \] So, 7,315 selections will contain no defective calculators.