Question: A jewelry store chain with 5 stores in state A, 10 stores in state B, and 12 in state C is planning…

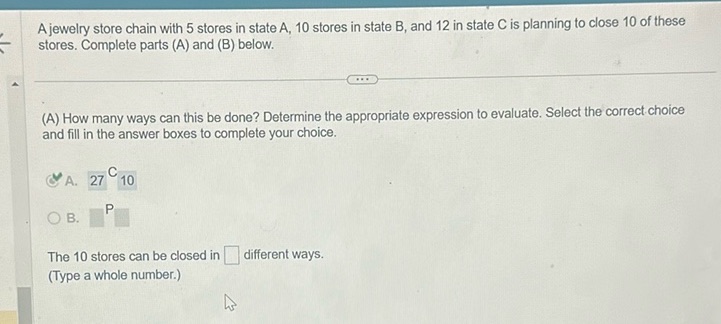
A jewelry store chain with 5 stores in state A, 10 stores in state B, and 12 in state C is planning to close 10 of these stores. Complete parts (A) and (B) below.

(A) How many ways can this be done? Determine the appropriate expression to evaluate. Select the correct choice and fill in the answer boxes to complete your choice.

A. 27 C 10 B. P

The 10 stores can be closed in different ways. (Type a whole number.)

Solution

To solve this problem, we need to determine how many ways we can choose 10 stores to close out of the total 27 stores. The expression to evaluate is the combination formula, which is: \[ \binom{n}{r} = \frac{n!}{r!(n-r)!} \] Here, \( n = 27 \) (total stores) and \( r = 10 \) (stores to close). Substitute the values into the combination formula: \[ \binom{27}{10} = \frac{27!}{10!(27-10)!} \] \[ = \frac{27!}{10! \times 17!} \] Now, we calculate it: \[ = \frac{27 \times 26 \times 25 \times 24 \times 23 \times 22 \times 21 \times 20 \times 19 \times 18}{10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} \] \[ = 17383860 \] Therefore, the 10 stores can be closed in 17,383,860 different ways.