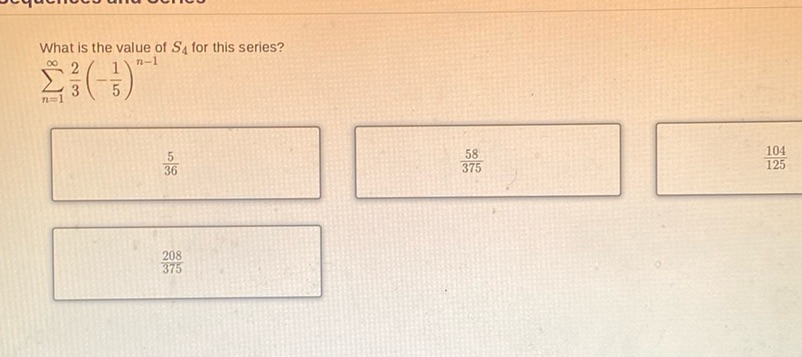
Question: What is the value of \( S_4 \) for this series? \[ \sum_{n=1}^{\infty} \frac{2}{3} \left(…

What is the value of \( S_4 \) for this series?

\[ \sum_{n=1}^{\infty} \frac{2}{3} \left( -\frac{1}{5} \right)^{n-1} \]

Options:

• \(\frac{5}{36}\)
• \(\frac{58}{375}\)
• \(\frac{104}{125}\)
• \(\frac{208}{375}\)

Solution

To find the value of \( S_4 \) for the series \[ \sum_{n=1}^{\infty} \frac{2}{3} \left( -\frac{1}{5} \right)^{n-1} \] we first recognize this as an infinite geometric series. The general term of a geometric series is given by: \[ a_n = a \cdot r^{n-1} \] where \( a \) is the first term and \( r \) is the common ratio. The first term \( a \) is \(\frac{2}{3}\), and the common ratio \( r \) is \(-\frac{1}{5}\). To find \( S_4 \), the sum of the first four terms, we calculate: \[ S_4 = a_1 + a_2 + a_3 + a_4 \] Calculate each term: \( a_1 = \frac{2}{3} \cdot \left(-\frac{1}{5}\right)^{0} = \frac{2}{3} \) \( a_2 = \frac{2}{3} \cdot \left(-\frac{1}{5}\right)^{1} = -\frac{2}{15} \) \( a_3 = \frac{2}{3} \cdot \left(-\frac{1}{5}\right)^{2} = \frac{2}{75} \) \( a_4 = \frac{2}{3} \cdot \left(-\frac{1}{5}\right)^{3} = -\frac{2}{375} \) Now, add these terms: \[ S_4 = \frac{2}{3} - \frac{2}{15} + \frac{2}{75} - \frac{2}{375} \] Find a common denominator, which is 375: \[ S_4 = \frac{250}{375} - \frac{50}{375} + \frac{10}{375} - \frac{2}{375} \] Combine the fractions: \[ S_4 = \frac{250 - 50 + 10 - 2}{375} = \frac{208}{375} \] The value of \( S_4 \) is \(\frac{208}{375}\).