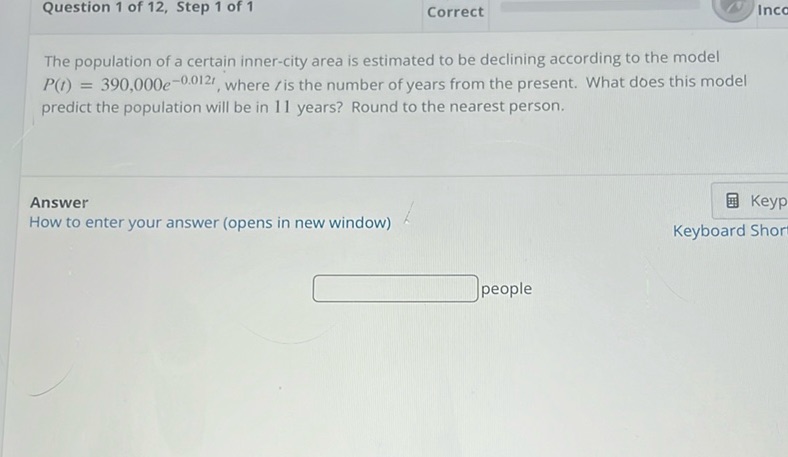
Question: The population of a certain inner-city area is estimated to be declining according to the model \(…

The population of a certain inner-city area is estimated to be declining according to the model \( P(t) = 390,000e^{-0.012t} \), where \( t \) is the number of years from the present. What does this model predict the population will be in 11 years? Round to the nearest person.

Answer

How to enter your answer (opens in new window)

people

Solution

To determine the population in 11 years using the given model, we use the formula: \[ P(t) = 390,000e^{-0.01t} \] Substitute \( t = 11 \) into the equation: \[ P(11) = 390,000e^{-0.01 \times 11} \] Calculate the exponent: \[ -0.01 \times 11 = -0.11 \] So, the equation becomes: \[ P(11) = 390,000e^{-0.11} \] Now, calculate \( e^{-0.11} \): \[ e^{-0.11} \approx 0.8958 \] Then multiply by 390,000: \[ P(11) = 390,000 \times 0.8958 \approx 349,362 \] The predicted population in 11 years, rounded to the nearest person, is 349,362 people.