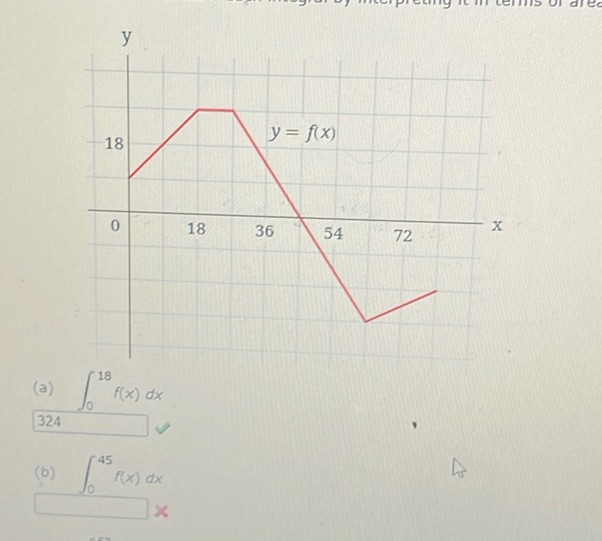
Question: The image shows a graph of a function \( y = f(x) \) plotted on a coordinate plane. The x-axis…

The image shows a graph of a function \( y = f(x) \) plotted on a coordinate plane. The x-axis ranges from 0 to 72, and the y-axis ranges from 0 to 18. The function \( f(x) \) is represented by a red line that starts at the origin (0,0), rises to a peak at (18, 18), then decreases to (36, 0), continues to decrease to (54, -18), and finally increases to (72, -6).

Below the graph, there are two integrals to be evaluated:

(a) \(\int_{0}^{18} f(x) \, dx\)

(b) \(\int_{0}^{45} f(x) \, dx\)

The answer for (a) is given as 324, which is marked as correct. The answer for (b) is marked as incorrect.

Solution

To solve the integral problem \(\int_{0}^{45} f(x) \, dx\) using the graph, we interpret the integral as the area under the curve from \(x=0\) to \(x=45\). 1. Identify Shapes and Calculate Area from 0 to 18: The area from \(x=0\) to \(x=18\) is a triangle with a base of 18 and a height of 18. \[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 18 \times 18 = 162 \] 2. Area from 18 to 36: The area from \(x=18\) to \(x=36\) is a trapezoid with bases of 18 and 0 and a height of 18. \[ \text{Area} = \frac{1}{2} \times (\text{base}1 + \text{base}2) \times \text{height} = \frac{1}{2} \times (18 + 0) \times 18 = 162 \] 3. Area from 36 to 45: The area from \(x=36\) to \(x=45\) is a right triangle with a base of 9 and a height of 18. \[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 9 \times 18 = 81 \] 4. Total Area Calculation from 0 to 45: \[ \int{0}^{45} f(x) \, dx = 162 + 162 + 81 = 405 \] The correct value for \(\int{0}^{45} f(x) \, dx\) is 405.