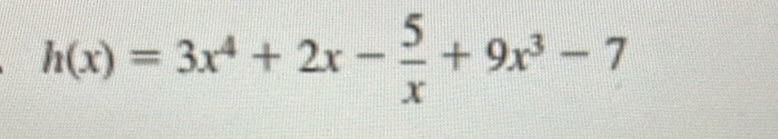
Question: The image contains a mathematical function: \[ h(x) = 3x^4 + 2x - \frac{5}{x} + 9x^3 - 7 \]

The image contains a mathematical function:

\[ h(x) = 3x^4 + 2x - \frac{5}{x} + 9x^3 - 7 \]

Solution

To differentiate the function \( h(x) = 3x^4 + 2x - \frac{5}{x} + 9x^3 - 7 \), follow these steps: First, recall the basic derivatives: - The derivative of \( x^n \) is \( nx^{n-1} \). - The derivative of a constant \( c \) is 0. - The derivative of \( \frac{1}{x} \) is \( -\frac{1}{x^2} \). Apply these rules to each term: Differentiate \( 3x^4 \): \[ \frac{d}{dx}(3x^4) = 12x^3 \] Differentiate \( 2x \): \[ \frac{d}{dx}(2x) = 2 \] Differentiate \( -\frac{5}{x} \): \[ \frac{d}{dx}\left(-\frac{5}{x}\right) = -5 \cdot \frac{d}{dx}(x^{-1}) = -5(-x^{-2}) = \frac{5}{x^2} \] Differentiate \( 9x^3 \): \[ \frac{d}{dx}(9x^3) = 27x^2 \] Differentiate the constant \(-7\): \[ \frac{d}{dx}(-7) = 0 \] Combine all these derivatives: \[ h’(x) = 12x^3 + 2 + \frac{5}{x^2} + 27x^2 \]