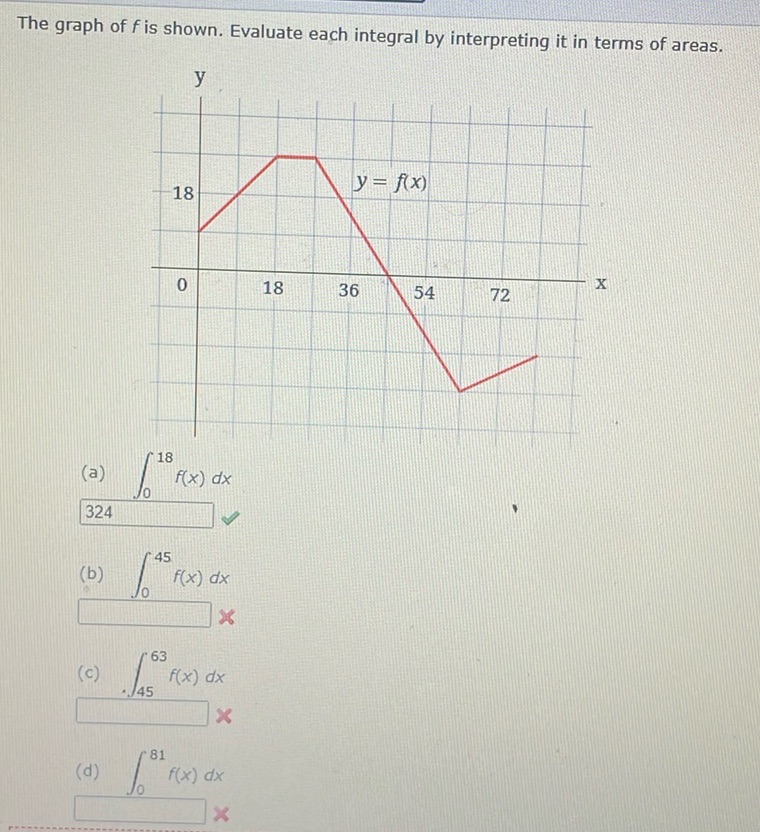
Question: The graph of \( f \) is shown. Evaluate each integral by interpreting it in terms of areas. \[…

The graph of \( f \) is shown. Evaluate each integral by interpreting it in terms of areas.

\[ \begin{array}{c} \text{y} \\ \begin{tikzpicture}[scale=0.5] \draw[help lines] (-1,-1) grid (10,10); \draw[->] (-1,0) — (10,0) node[right] {$x$}; \draw[->] (0,-1) — (0,10) node[above] {$y$}; \draw[thick,red] (0,0) — (3,6) — (6,9) — (9,0); \draw (3,6) node[above right] {$y = f(x)$}; \draw (0,0) node[below left] {$0$}; \draw (3,0) node[below] {$18$}; \draw (6,0) node[below] {$36$}; \draw (9,0) node[below] {$54$}; \draw (10,0) node[below] {$72$}; \draw (0,3) node[left] {$18$}; \end{tikzpicture} \end{array} \]

(a) \(\int_{0}^{18} f(x) \, dx\)

324

(b) \(\int_{0}^{45} f(x) \, dx\)

(c) \(\int_{45}^{63} f(x) \, dx\)

(d) \(\int_{0}^{81} f(x) \, dx\)

Solution

The question involves evaluating definite integrals by interpreting the graph as areas under the curve. (a) \(\int_0^{18} f(x) \, dx = 324\) This integral is already evaluated correctly. Let’s move to the next parts. For the graph, we calculate the area of geometric shapes formed by the graph between the given limits. (b) \(\int_0^{45} f(x) \, dx\) From 0 to 18, we have a rectangle. Area = \(18 \times 18 = 324\). From 18 to 36, we have a rectangle. Base = 18, height = 18. Area = \(18 \times 18 = 324\). From 36 to 45, we have a trapezoid. Average height = \(\frac{18 + 0}{2} = 9\), base = 9. Area = \(9 \times 9 = 81\). Total area = \(324 + 324 + 81 = 729\). (c) \(\int_{45}^{63} f(x) \, dx\) From 45 to 54, we have a triangle. Area = \(\frac{1}{2} \times 9 \times 18 = 81\). From 54 to 63, we have a triangle. Area = \(\frac{1}{2} \times 9 \times 18 = 81\). Total area = \(81 + 81 = 162\), but since these areas are under the x-axis, they should be negative. Final area = \(-162\). (d) \(\int_0^{81} f(x) \, dx\) \(\int_0^{45} f(x) \, dx = 729\) \(\int_{45}^{63} f(x) \, dx = -162\) From 63 to 72, we have a triangle. Area = \(\frac{1}{2} \times 9 \times 18 = 81\), negative since below x-axis. From 72 to 81, we have a triangle. Area = \(\frac{1}{2} \times 9 \times 9 = 40.5\). Final area = \(729 - 162 - 81 - 40.5 = 445.5\).