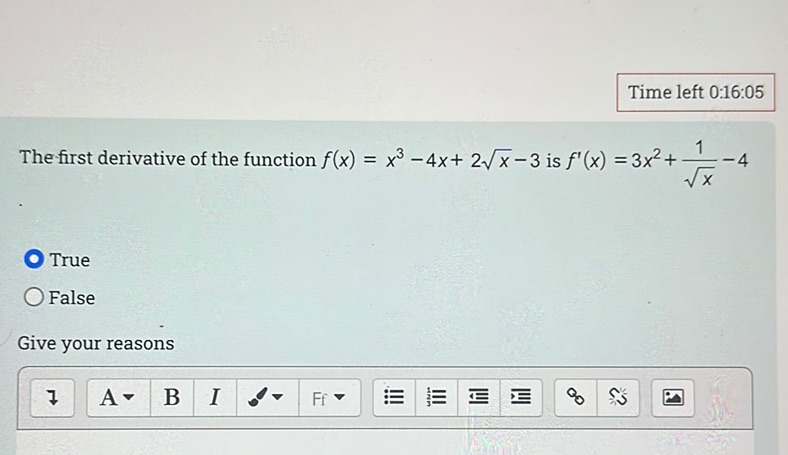
Question: The first derivative of the function \( f(x) = x^3 - 4x + 2\sqrt{x} - 3 \) is \( f’(x) = 3x^2 +…

The first derivative of the function \( f(x) = x^3 - 4x + 2\sqrt{x} - 3 \) is \( f’(x) = 3x^2 + \frac{1}{\sqrt{x}} - 4 \)

True

False

Give your reasons

Solution

The statement claims that the first derivative of the function is correct. Let’s verify its validity step by step. \[ f(x) = x^{3} - 4x + 2\sqrt{x - 3} \] To find the derivative \( f’(x) \), differentiate each term with respect to \( x \): \[ f’(x) = \frac{d}{dx}\left(x^{3}\right) - \frac{d}{dx}\left(4x\right) + \frac{d}{dx}\left(2\sqrt{x - 3}\right) & \] \[ f’(x) = 3x^{2} - 4 + \frac{2}{2\sqrt{x - 3}} & \] Simplify the derivative: \[ f’(x) = 3x^{2} - 4 + \frac{1}{\sqrt{x - 3}} & \] Comparing this with the provided derivative: \[ f’(x) = 3x^{2} + \frac{1}{\sqrt{x}} - 4 & \] The discrepancy lies in the third term. The correct derivative has \( \frac{1}{\sqrt{x - 3}} \) instead of \( \frac{1}{\sqrt{x}} \). Therefore, the original statement is False.