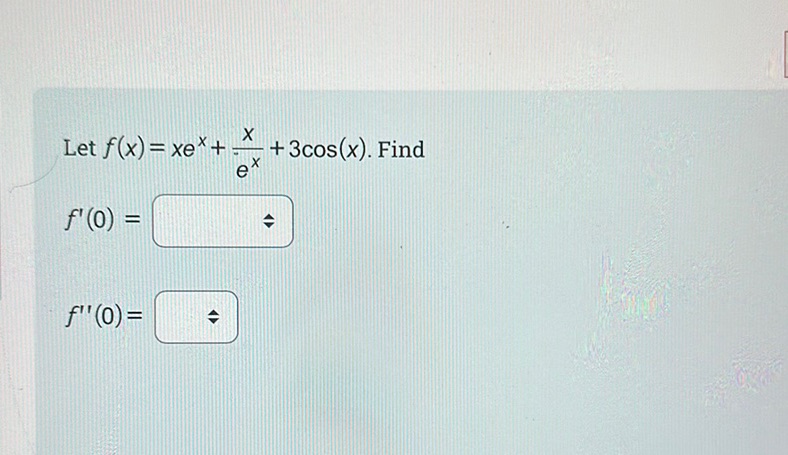
Question: Let \( f(x) = xe^x + \frac{x}{e^x} + 3\cos(x) \). Find \( f’(0) = \boxed{\phantom{xxxx}}…

Let \( f(x) = xe^x + \frac{x}{e^x} + 3\cos(x) \). Find

\( f’(0) = \boxed{\phantom{xxxx}} \)

\( f”(0) = \boxed{\phantom{xxxx}} \)

Solution

To find \( f’(0) \) and \( f”(0) \), we first need to differentiate \( f(x) \). Given: \[ f(x) = xe^x + \frac{x}{e^x} + 3\cos(x) \] First, find \( f’(x) \). The derivative of \( xe^x \) using the product rule: \[ \frac{d}{dx}[xe^x] = e^x + xe^x \] The derivative of \( \frac{x}{e^x} \) using the quotient rule: \[ \frac{d}{dx}\left(\frac{x}{e^x}\right) = \frac{e^x - xe^x}{(e^x)^2} = \frac{1 - x}{e^x} \] The derivative of \( 3\cos(x) \): \[ \frac{d}{dx}[3\cos(x)] = -3\sin(x) \] Combine these results to get \( f’(x) \): \[ f’(x) = e^x + xe^x + \frac{1-x}{e^x} - 3\sin(x) \] Now substitute \( x = 0 \) to find \( f’(0) \): \[ f’(0) = e^0 + 0 \cdot e^0 + \frac{1-0}{e^0} - 3\sin(0) \] \[ f’(0) = 1 + 0 + 1 - 0 = 2 \] Next, find \( f”(x) \) by differentiating \( f’(x) \). Differentiate each term: The derivative of \( e^x \) is \( e^x \). The derivative of \( xe^x \) using the product rule: \[ \frac{d}{dx}[xe^x] = e^x + xe^x \] The derivative of \( \frac{1-x}{e^x} \) using the quotient rule: \[ \frac{d}{dx}\left(\frac{1-x}{e^x}\right) = \frac{-(1-x)e^x - (-1)e^x}{(e^x)^2} = \frac{x}{e^x} \] The derivative of \( -3\sin(x) \): \[ \frac{d}{dx}[-3\sin(x)] = -3\cos(x) \] Combine these results to get \( f”(x) \): \[ f”(x) = e^x + e^x + xe^x + \frac{x}{e^x} - 3\cos(x) \] Simplify: \[ f”(x) = 2e^x + xe^x + \frac{x}{e^x} - 3\cos(x) \] Now substitute \( x = 0 \) to find \( f”(0) \): \[ f”(0) = 2e^0 + 0 \cdot e^0 + \frac{0}{e^0} - 3\cos(0) \] \[ f”(0) = 2 + 0 + 0 - 3 \cdot 1 \] \[ f”(0) = 2 - 3 = -1 \] Thus, the answers are: \( f’(0) = 2 \) \( f”(0) = -1 \)