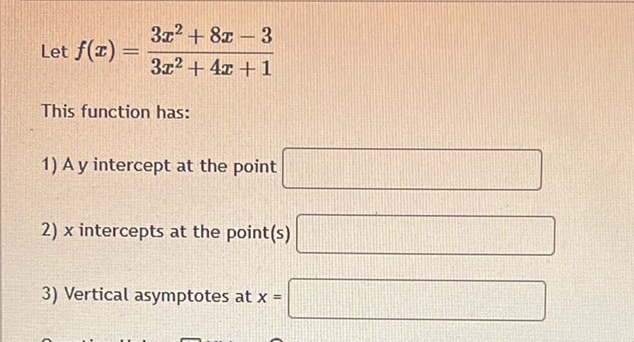
Question: Let \( f(x) = \frac{3x^2 + 8x - 3}{3x^2 + 4x + 1} \) This function has: 1) A y-intercept at…

Let \( f(x) = \frac{3x^2 + 8x - 3}{3x^2 + 4x + 1} \)

This function has:

1. A y-intercept at the point

2. x-intercepts at the point(s)

3. Vertical asymptotes at \( x = \)

Solution

Step 1: Find the y-intercept. To find the y-intercept, evaluate \( f(0) \): \[ f(0) = \frac{3(0)^2 + 8(0) - 3}{3(0)^2 + 4(0) + 1} = \frac{-3}{1} = -3 & \] Therefore, the y-intercept is at the point \( (0, -3) \). Step 2: Find the x-intercepts. To find the x-intercepts, set \( f(x) = 0 \), which means the numerator must be zero: \[ 3x^2 + 8x - 3 = 0 & \] Solve the quadratic equation using the quadratic formula: \[ x = \frac{-8 \pm \sqrt{8^2 - 4 \cdot 3 \cdot (-3)}}{2 \cdot 3} = \frac{-8 \pm \sqrt{64 + 36}}{6} = \frac{-8 \pm \sqrt{100}}{6} = \frac{-8 \pm 10}{6} & \] Thus, the solutions are: \[ x = \frac{2}{6} = \frac{1}{3} \quad \text{and} \quad x = \frac{-18}{6} = -3 & \] Therefore, the x-intercepts are at the points \( \left( \frac{1}{3}, 0 \right) \) and \( (-3, 0) \). Step 3: Find the vertical asymptotes. Vertical asymptotes occur where the denominator is zero and the numerator is not zero. Set the denominator equal to zero: \[ 3x^2 + 4x + 1 = 0 & \] Solve the quadratic equation: \[ x = \frac{-4 \pm \sqrt{4^2 - 4 \cdot 3 \cdot 1}}{2 \cdot 3} = \frac{-4 \pm \sqrt{16 - 12}}{6} = \frac{-4 \pm \sqrt{4}}{6} = \frac{-4 \pm 2}{6} & \] Thus, the solutions are: \[ x = \frac{-2}{6} = -\frac{1}{3} \quad \text{and} \quad x = \frac{-6}{6} = -1 & \] Therefore, the vertical asymptotes are at \( x = -\frac{1}{3} \) and \( x = -1 \).