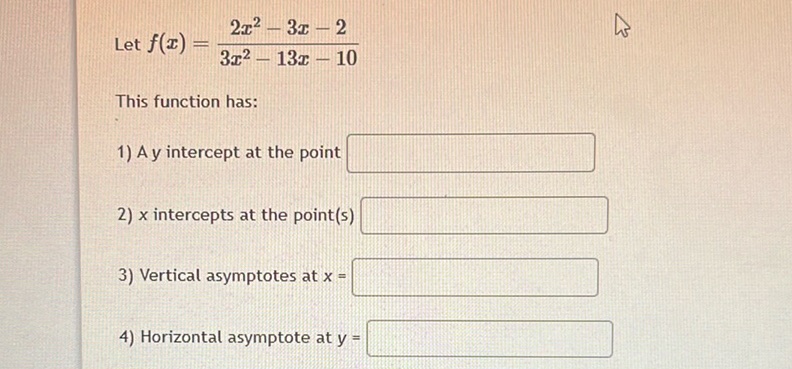
Question: Let \( f(x) = \frac{2x^2 - 3x - 2}{3x^2 - 13x - 10} \) This function has: 1) A y-intercept at…

Let \( f(x) = \frac{2x^2 - 3x - 2}{3x^2 - 13x - 10} \)

This function has:

1. A y-intercept at the point

2. x-intercepts at the point(s)

3. Vertical asymptotes at \( x = \)

4. Horizontal asymptote at \( y = \)

Solution

To find the properties of the function \( f(x) = \frac{2x^2 - 3x - 2}{3x^2 - 13x - 10} \), let’s solve each part step by step. 1) Y-intercept at the point To find the y-intercept, set \( x = 0 \): \[ f(0) = \frac{2(0)^2 - 3(0) - 2}{3(0)^2 - 13(0) - 10} = \frac{-2}{-10} = \frac{1}{5} & \] Answer: The y-intercept is at the point \( \left(0, \frac{1}{5}\right) \). 2) X-intercepts at the point(s) To find the x-intercepts, set the numerator equal to zero: \[ 2x^2 - 3x - 2 = 0 & \] Solving the quadratic equation: \[ x = \frac{3 \pm \sqrt{(-3)^2 - 4(2)(-2)}}{2(2)} = \frac{3 \pm \sqrt{9 + 16}}{4} = \frac{3 \pm 5}{4} & \] So, the solutions are: \[ x = \frac{3 + 5}{4} = 2 \\ x = \frac{3 - 5}{4} = -\frac{1}{2} & \] Answer: The x-intercepts are at the points \( \left(2, 0\right) \) and \( \left(-\frac{1}{2}, 0\right) \). 3) Vertical asymptotes at \( x = \) To find the vertical asymptotes, set the denominator equal to zero: \[ 3x^2 - 13x - 10 = 0 & \] Solving the quadratic equation: \[ x = \frac{13 \pm \sqrt{(-13)^2 - 4(3)(-10)}}{2(3)} = \frac{13 \pm \sqrt{169 + 120}}{6} = \frac{13 \pm \sqrt{289}}{6} & \] So, the solutions are: \[ x = \frac{13 + 17}{6} = 5 \\ x = \frac{13 - 17}{6} = -\frac{2}{3} & \] Answer: The vertical asymptotes are at \( x = 5 \) and \( x = -\frac{2}{3} \). 4) Horizontal asymptote at \( y = \) For the horizontal asymptote of a rational function where the degrees of the numerator and denominator are equal, it is the ratio of the leading coefficients: \[ y = \frac{2}{3} & \] Answer: The horizontal asymptote is at \( y = \frac{2}{3} \).