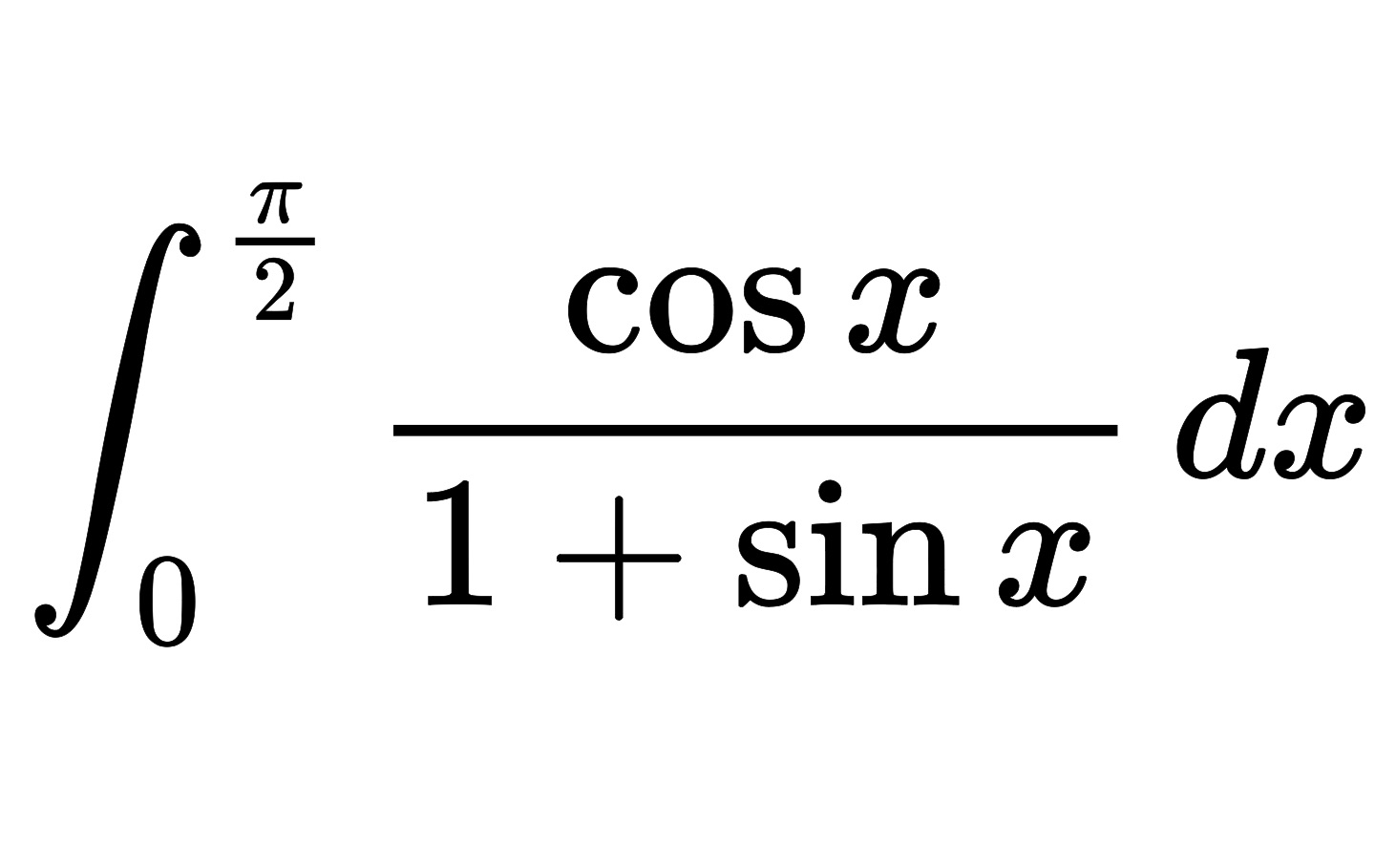
Question: (\int_{0}^{\frac{\pi}{2}} \frac{\cos x}{1 + \sin x} dx\)…

\(\int_{0}^{\frac{\pi}{2}} \frac{\cos x}{1 + \sin x} dx\)

Solution

To solve the integral

\[ \int_0^{\frac{\pi}{2}} \frac{\cos x}{1 + \sin x} \, dx \]

we’ll use a substitution method.

Let

\[ u = 1 + \sin x \]

Then,

\[ du = \cos x \, dx \]

Substituting in the limits:

When \( x = 0 \), \( u = 1 + \sin 0 = 1 \).

When \( x = \frac{\pi}{2} \), \( u = 1 + \sin \frac{\pi}{2} = 2 \).

Now the integral becomes:

\[ \int_1^2 \frac{1}{u} \, du \]

The antiderivative of \(\frac{1}{u}\) is

\[ \ln |u| \]

So, we have:

\[ \int_1^2 \frac{1}{u} \, du = \ln |u| \Big|_1^2 \]

Evaluating this, we get:

\[ \ln |2| - \ln |1| = \ln 2 - \ln 1 = \ln 2 \]

Therefore, the value of the integral is

\[ \ln 2 \]