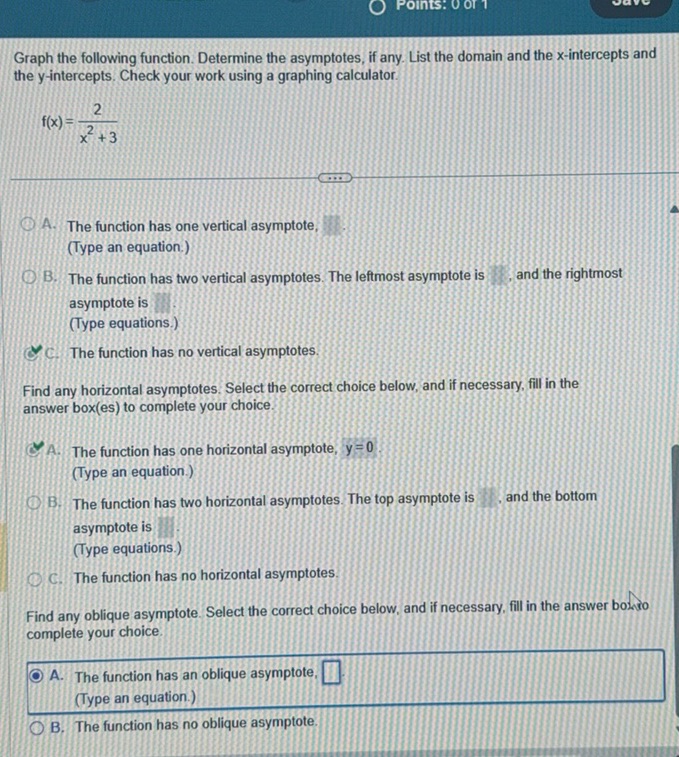
Question: Graph the following function. Determine the asymptotes, if any. List the domain and the…

Graph the following function. Determine the asymptotes, if any. List the domain and the x-intercepts and the y-intercepts. Check your work using a graphing calculator.

\[ f(x) = \frac{2}{x^2 + 3} \]

A. The function has one vertical asymptote, (Type an equation.)

B. The function has two vertical asymptotes. The leftmost asymptote is , and the rightmost asymptote is (Type equations.)

C. The function has no vertical asymptotes.

Find any horizontal asymptotes. Select the correct choice below, and if necessary, fill in the answer box(es) to complete your choice.

A. The function has one horizontal asymptote, \( y = 0 \) (Type an equation.)

B. The function has two horizontal asymptotes. The top asymptote is , and the bottom asymptote is (Type equations.)

C. The function has no horizontal asymptotes.

Find any oblique asymptote. Select the correct choice below, and if necessary, fill in the answer box(es) to complete your choice.

A. The function has an oblique asymptote, (Type an equation.)

B. The function has no oblique asymptote.

Solution

Let’s solve the problem step by step. First, let’s analyze the function: \[ f(x) = \frac{2}{x^2 + 3} \] 1. Domain of the Function The domain consists of all real numbers except those that make the denominator zero. \[ x^2 + 3 = 0 \] \[ x^2 = -3 \] Since \( x^2 \) cannot be negative, there are no real solutions. Domain: \[ \text{All real numbers } \mathbb{R} \] 2. Vertical Asymptotes Vertical asymptotes occur where the denominator is zero. As shown above, \( x^2 + 3 = 0 \) has no real solutions. Vertical Asymptotes: \[ \text{None} \] 3. Horizontal Asymptotes For rational functions, if the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is \( y = 0 \). Here, the degree of the numerator is 0, and the degree of the denominator is 2. Horizontal Asymptote: \[ y = 0 \] 4. Oblique Asymptotes Oblique asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator. In this case, the degree of the numerator is less than the degree of the denominator. Oblique Asymptote: \[ \text{None} \] 5. X-Intercepts X-intercepts occur where \( f(x) = 0 \). \[ \frac{2}{x^2 + 3} = 0 \] Since the numerator is 2 and never zero, there are no x-intercepts. X-Intercepts: \[ \text{None} \] 6. Y-Intercepts Y-intercepts occur where \( x = 0 \). \[ f(0) = \frac{2}{0^2 + 3} = \frac{2}{3} \] Y-Intercept: \[ \left(0, \frac{2}{3}\right) \] Summary: \[ \begin{cases} \text{Domain: } \mathbb{R} & \\ \text{Vertical Asymptotes: None} & \\ \text{Horizontal Asymptote: } y = 0 & \\ \text{Oblique Asymptote: None} & \\ \text{X-Intercepts: None} & \\ \text{Y-Intercept: } \left(0, \frac{2}{3}\right) & \end{cases} \]