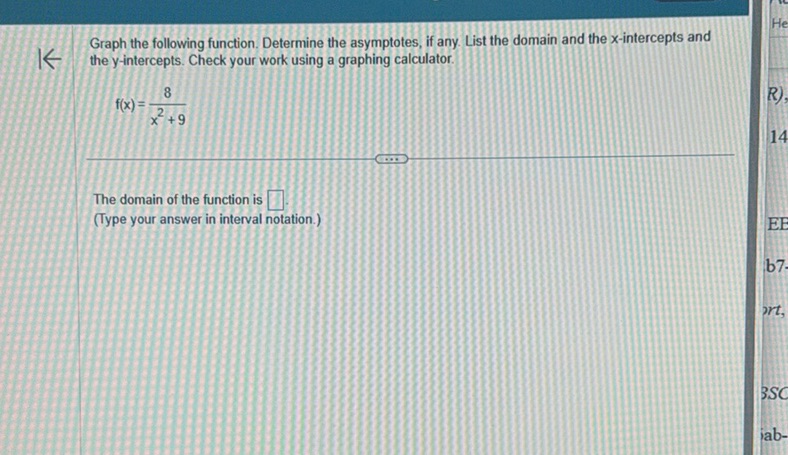
Question: Graph the following function. Determine the asymptotes, if any. List the domain and the…

Graph the following function. Determine the asymptotes, if any. List the domain and the x-intercepts and the y-intercepts. Check your work using a graphing calculator.

\[ f(x) = \frac{8}{x^2 + 9} \]

The domain of the function is \(\boxed{\quad}\).

(Type your answer in interval notation.)

Solution

Step 1: Graph the function To graph the function \( f(x) = \frac{8}{x^2 + 9} \), observe that it is a rational function where the denominator is always positive since \( x^2 + 9 \) is always greater than zero. Therefore, the function will always be positive and never cross the x-axis. Step 2: Determine the asymptotes, if any Since the denominator \( x^2 + 9 \) is never zero, there are no vertical asymptotes. As \( x \) approaches infinity or negative infinity, the function \( f(x) \) approaches zero. Therefore, the horizontal asymptote is: \[ y = 0 & \] Step 3: List the domain The denominator \( x^2 + 9 \) is never zero, so the function is defined for all real numbers. Thus, the domain in interval notation is: \[ (-\infty, \infty) & \] Step 4: Find the x-intercepts and y-intercepts - x-intercepts: Set \( f(x) = 0 \) and solve for \( x \): \[ 0 = \frac{8}{x^2 + 9} \] Since the numerator is 8 (a non-zero constant), there are no real solutions. Therefore, there are no x-intercepts. - y-intercept: Set \( x = 0 \) and solve for \( f(0) \): \[ f(0) = \frac{8}{0^2 + 9} = \frac{8}{9} & \] So, the y-intercept is \( \left(0, \frac{8}{9}\right) \). Step 5: Check the work using a graphing calculator To verify the graph and the properties of the function: 1. Enter the function \( f(x) = \frac{8}{x^2 + 9} \) into the graphing calculator. 2. Observe the graph to confirm that it is a smooth curve above the x-axis, approaching the horizontal asymptote \( y = 0 \) as \( x \) moves away from zero in both directions. 3. Verify that the y-intercept is at \( \left(0, \frac{8}{9}\right) \) and that there are no x-intercepts.