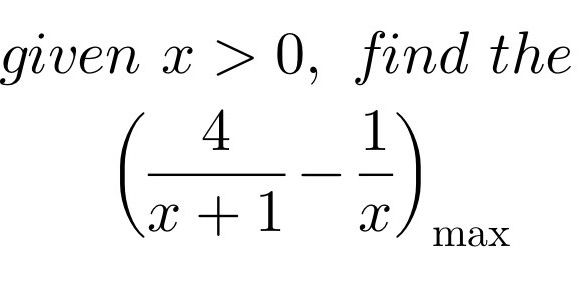
Question: Given \( x > 0 \), find the maximum of \(\left( \frac{4}{x + 1} - \frac{1}{x} \right)\).

Given \( x > 0 \), find the maximum of \(\left( \frac{4}{x + 1} - \frac{1}{x} \right)\).

Solution

To find the maximum value of the function \[ f(x) = \frac{4}{x+1} - \frac{1}{x}, \] we first find the derivative of \( f(x) \) with respect to \( x \). The derivative of \( f(x) \) is \[ f’(x) = \frac{d}{dx}\left(\frac{4}{x+1} - \frac{1}{x}\right). \] Use the quotient rule for derivatives: for a function \( \frac{u}{v} \), the derivative is given by \[ \frac{d}{dx}\left(\frac{u}{v}\right) = \frac{u’v - uv’}{v^2}. \] Applying this to both terms, we have: For \(\frac{4}{x+1}\): \[ u = 4, \quad v = x+1, \quad u’ = 0, \quad v’ = 1, \] \[ \Rightarrow \frac{d}{dx}\left(\frac{4}{x+1}\right) = \frac{0 \cdot (x+1) - 4 \cdot 1}{(x+1)^2} = -\frac{4}{(x+1)^2}. \] For \(\frac{1}{x}\): \[ u = 1, \quad v = x, \quad u’ = 0, \quad v’ = 1, \] \[ \Rightarrow \frac{d}{dx}\left(-\frac{1}{x}\right) = -\frac{0 \cdot x - 1 \cdot 1}{x^2} = \frac{1}{x^2}. \] Thus, \[ f’(x) = -\frac{4}{(x+1)^2} + \frac{1}{x^2}. \] Set the derivative equal to zero to find the critical points: \[ -\frac{4}{(x+1)^2} + \frac{1}{x^2} = 0. \] Solving for \( x \), we get: \[ \frac{1}{x^2} = \frac{4}{(x+1)^2}. \] Cross-multiply: \[ (x+1)^2 = 4x^2. \] Expand and simplify: \[ x^2 + 2x + 1 = 4x^2, \] \[ 3x^2 - 2x - 1 = 0. \] Use the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) with \( a = 3, b = -2, c = -1 \): \[ x = \frac{-(-2) \pm \sqrt{(-2)^2 - 4 \cdot 3 \cdot (-1)}}{2 \cdot 3}, \] \[ x = \frac{2 \pm \sqrt{4 + 12}}{6}, \] \[ x = \frac{2 \pm \sqrt{16}}{6}, \] \[ x = \frac{2 \pm 4}{6}. \] The solutions are \( x = 1 \) and \( x = -\frac{1}{3} \). Since \( x > 0 \), we have \( x = 1 \). To confirm it is a maximum, check the second derivative \( f”(x) \) at \( x = 1 \): \[ f”(x) = \frac{d}{dx}\left(-\frac{4}{(x+1)^2} + \frac{1}{x^2}\right). \] Calculate: \[ f”(x) = \left(\frac{8}{(x+1)^3} - \frac{2}{x^3}\right). \] Evaluate \( f”(1) \): \[ f”(1) = \frac{8}{2^3} - \frac{2}{1^3}, \] \[ f”(1) = 1 - 2 = -1. \] Since \( f”(1) < 0 \), \( x = 1 \) is a local maximum. Calculate \( f(1) \): \[ f(1) = \frac{4}{2} - \frac{1}{1} = 2 - 1 = 1. \] The maximum value of the function is 1.