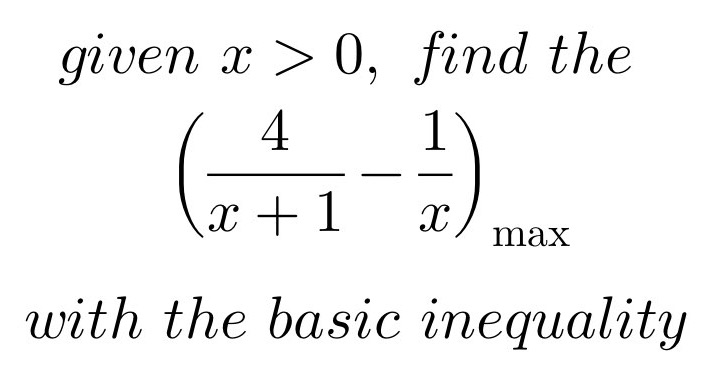
Question: Given \( x > 0 \), find the maximum of \(\left( \frac{4}{x + 1} - \frac{1}{x} \right)\)…

Given \( x > 0 \), find the maximum of \(\left( \frac{4}{x + 1} - \frac{1}{x} \right)\) with the basic inequality.

Solution

To find the maximum of \[ f(x) = \frac{4}{x+1} - \frac{1}{x} \] we can use the inequality \( AM \geq GM \) (Arithmetic Mean - Geometric Mean inequality). Apply \( AM \geq GM \) to the numbers \( x \) and \( 1 \): \[ \frac{x + 1}{2} \geq \sqrt{x \cdot 1} \] This implies: \[ \frac{x + 1}{2} \geq \sqrt{x} \] which can be rearranged as: \[ x + 1 \geq 2\sqrt{x} \] Square both sides: \[ (x + 1)^2 \geq 4x \] This simplifies to: \[ x^2 + 2x + 1 \geq 4x \] Rearrange the terms: \[ x^2 - 2x + 1 \geq 0 \] Complete the square: \[ (x-1)^2 \geq 0 \] Since \((x-1)^2 \geq 0\) is always true, equality holds when \(x = 1\). Now evaluate \(f(x)\) at \(x = 1\): \[ f(1) = \frac{4}{1+1} - \frac{1}{1} = \frac{4}{2} - 1 = 2 - 1 = 1 \] Therefore, the maximum value of \(\frac{4}{x+1} - \frac{1}{x}\), for \(x > 0\), is \(1\).