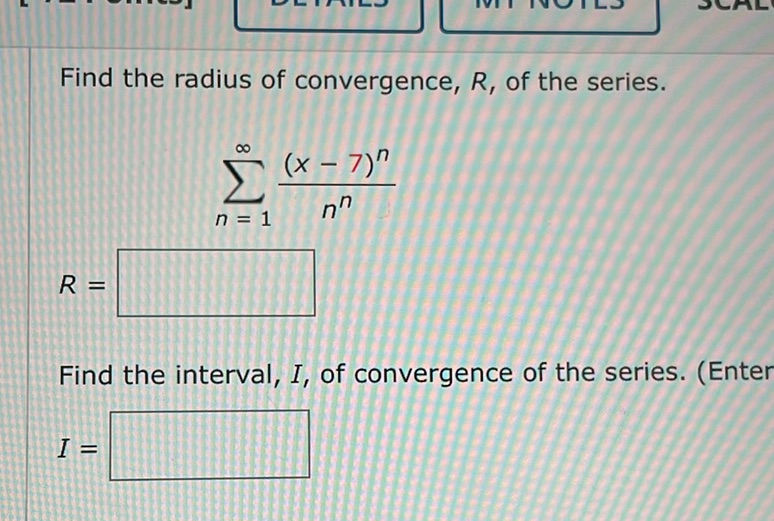
Question: Find the radius of convergence, \( R \), of the series. \[ \sum_{n=1}^{\infty}…

Find the radius of convergence, \( R \), of the series.

\[ \sum_{n=1}^{\infty} \frac{(x-7)^n}{n^n} \]

\( R = \boxed{\phantom{0}} \)

Find the interval, \( I \), of convergence of the series. (Enter your answer using interval notation.)

\( I = \boxed{\phantom{0}} \)

Solution

To find the radius of convergence, \( R \), and the interval of convergence, \( I \), for the series \[ \sum_{n=1}^{\infty} \frac{(x-7)^n}{n^n} \] Begin by applying the Root Test. \[ \lim_{n \to \infty} \sqrt[n]{\left| \frac{(x-7)^n}{n^n} \right|} = \lim_{n \to \infty} \frac{|x-7|}{n} = 0 \] Since the limit is \( 0 \), which is less than \( 1 \), the series converges for all real numbers \( x \). Therefore, the radius of convergence is \[ R = \infty \] And the interval of convergence is \[ I = (-\infty, \infty) \]