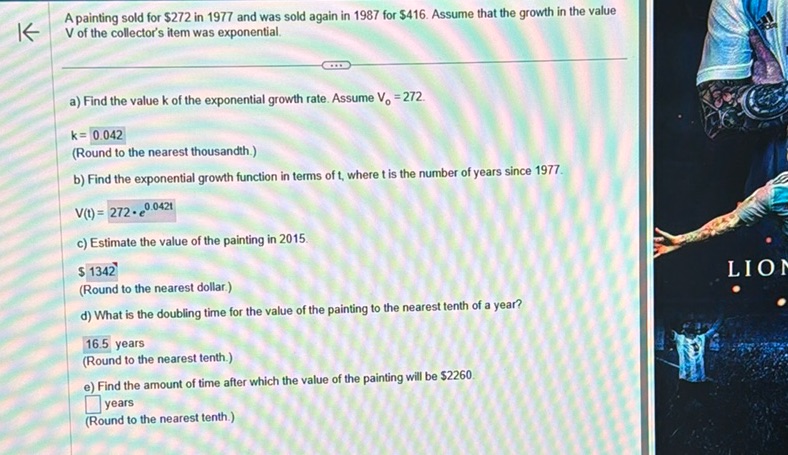
Question: A painting sold for $272 in 1977 and was sold again in 1987 for $416. Assume that the growth in the…

A painting sold for $272 in 1977 and was sold again in 1987 for $416. Assume that the growth in the value V of the collector’s item was exponential.

a) Find the value k of the exponential growth rate. Assume V_0 = 272.

k = 0.042 (Round to the nearest thousandth.)

b) Find the exponential growth function in terms of t, where t is the number of years since 1977.

V(t) = 272 * e^(0.042t)

C) Estimate the value of the painting in 2015.

$1342 (Round to the nearest dollar.)

d) What is the doubling time for the value of the painting to the nearest tenth of a year?

16.5 years (Round to the nearest tenth.)

e) Find the amount of time after which the value of the painting will be $2260.

□ years (Round to the nearest tenth.)

Solution

A painting sold for $272 in 1977 and was sold again in 1987 for $416. Assume that the growth in the value \( V \) of the collector’s item was exponential. a) Find the value \( k \) of the exponential growth rate. Assume \( V_0 = 272 \). Given: Initial value, \( V_0 = 272 \) Final value, \( V_{1987} = 416 \) Time, \( t = 1987 - 1977 = 10 \) years The formula for exponential growth is: \[ V(t) = V_0 \cdot e^{kt} \] Plugging in the values: \[ 416 = 272 \cdot e^{10k} \] \[ \frac{416}{272} = e^{10k} \] \[ \ln{\left(\frac{416}{272}\right)} = 10k \] \[ k = \frac{\ln{\left(\frac{416}{272}\right)}}{10} \] Calculating, \[ k \approx 0.042 \] b) Find the exponential growth function in terms of \( t \). The exponential growth function is: \[ V(t) = 272 \cdot e^{0.042t} \] c) Estimate the value of the painting in 2015. Time from 1977 to 2015 is \( t = 2015 - 1977 = 38 \) years. \[ V(38) = 272 \cdot e^{0.042 \cdot 38} \] Calculating, \[ V(38) \approx 1342 \] d) What is the doubling time for the value of the painting? We need to find \( t \) such that: \[ 2 \cdot 272 = 272 \cdot e^{0.042t} \] \[ 2 = e^{0.042t} \] \[ \ln{2} = 0.042t \] \[ t = \frac{\ln{2}}{0.042} \] Calculating, \[ t \approx 16.5 \] e) Find the amount of time after which the value of the painting will be $2260. \[ 2260 = 272 \cdot e^{0.042t} \] \[ \frac{2260}{272} = e^{0.042t} \] \[ \ln{\left(\frac{2260}{272}\right)} = 0.042t \] \[ t = \frac{\ln{\left(\frac{2260}{272}\right)}}{0.042} \] Calculating, \[ t \approx 44.9 \]