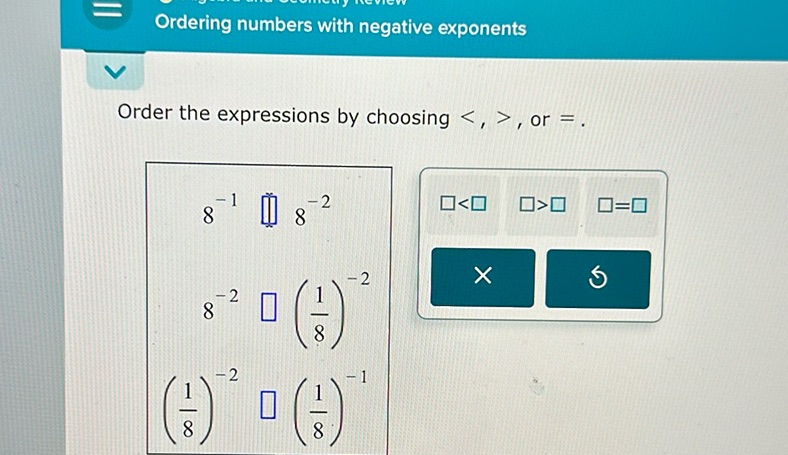
Question: Ordering numbers with negative exponents Order the expressions by choosing <, >, or =. 8^{-1} [ ]…

Ordering numbers with negative exponents Order the expressions by choosing <, >, or =. 8^{-1} [ ] 8^{-2} 8^{-2} [ ] (\frac{1}{8})^{-2} (\frac{1}{8})^{-2} [ ] (\frac{1}{8})^{-1}

Solution

Let’s compare the given expressions by evaluating each one. 1. Evaluate \(8^{-1}\): \[ 8^{-1} = \frac{1}{8} \] 2. Evaluate \(8^{-2}\): \[ 8^{-2} = \frac{1}{8^2} = \frac{1}{64} \] 3. Evaluate \(\left(\frac{1}{8}\right)^{-2}\): \[ \left(\frac{1}{8}\right)^{-2} = 8^2 = 64 \] 4. Evaluate \(\left(\frac{1}{8}\right)^{-1}\): \[ \left(\frac{1}{8}\right)^{-1} = 8 \] Now, order the expressions: \[ \frac{1}{64} < \frac{1}{8} < 8 < 64 \] Therefore, the order is: \(8^{-2}\) < \(8^{-1}\) < \(\left(\frac{1}{8}\right)^{-1}\) < \(\left(\frac{1}{8}\right)^{-2}\).