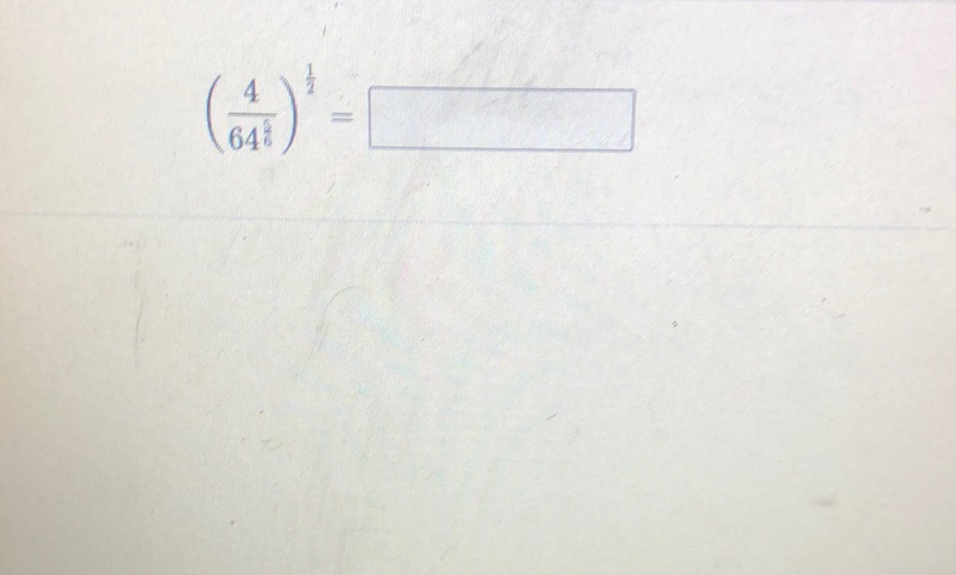
Question: (\[ \left( \frac{4}{64} \right)^{\frac{1}{2}} = \boxed{\phantom{0}} \]\)…

\(\[ \left( \frac{4}{64} \right)^{\frac{1}{2}} = \boxed{\phantom{0}} \]\)

Solution

The problem is to simplify the expression \(\left(\frac{4}{64}\right)^{\frac{1}{2}}\). First, simplify the fraction inside the parentheses: \[ \frac{4}{64} = \frac{1}{16} \] Next, the expression inside the parentheses becomes \(\frac{1}{16}\). Now take the square root: \[ \left(\frac{1}{16}\right)^{\frac{1}{2}} = \frac{1}{\sqrt{16}} = \frac{1}{4} \] Thus, the simplified answer is \(\frac{1}{4}\).