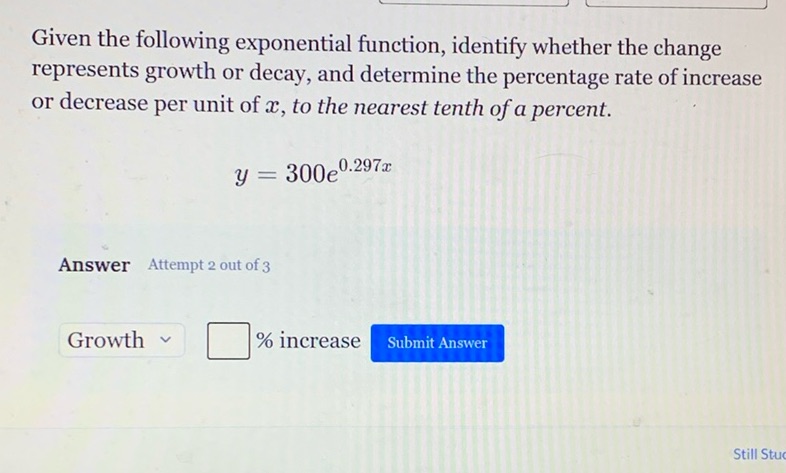
Question: Given the following exponential function, identify whether the change represents growth or decay,…

Given the following exponential function, identify whether the change represents growth or decay, and determine the percentage rate of increase or decrease per unit of \( x \), to the nearest tenth of a percent.

\[ y = 300e^{0.297x} \]

Answer Attempt 2 out of 3

Growth \(\square\) % increase Submit Answer

Solution

Given the exponential function: \[ y = 300e^{0.297x} \] First, identify whether the change represents growth or decay. Since the exponent \(0.297\) is positive, the function represents exponential growth. Next, determine the percentage rate of increase per unit of \(x\). The rate of growth \(r\) in the exponential function \(y = ae^{rx}\) is the coefficient of \(x\) in the exponent. Therefore, \(r = 0.297\). Convert this to a percentage: \[ \text{Percentage increase} = 0.297 \times 100\% \] Calculate the percentage: \[ \text{Percentage increase} = 29.7\% \] So, the change represents growth, with a percentage rate of increase of 29.7% per unit of \(x\).